Salze und Salzgemische: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 94: | Zeile 94: | ||
==Salzgemische, in denen Doppelsalze gebildet werden können== | ==Salzgemische, in denen Doppelsalze gebildet werden können== | ||
Die Betrachtung von Salzgemischen kann noch weiter ausgeführt werden. In vielen Salzmischungen können sich Doppelsalze bilden, also solche Salze, die drei oder mehr verschiedene Ionen enthalten. Wie bereits oben erwähnt, gibt es sowohl kongruent als auch inkongruent lösliche Doppelsalze. Zunächst soll ein Löslichkeitsdiagramm einer Mischung aus Na<sub>2</sub>SO<sub>4</sub> und MgSO<sub>4</sub> betrachtet werden (Abbildung 9), da sich in einem solchen Gemisch ein kongruent lösliches Doppelsalz ([[Astrakanit]] alias [[Astrakanit | Blödit]]; Na<sub>2</sub>Mg(SO<sub>4</sub>)<sub>2</sub>∙4H<sub>2</sub>O) bilden kann. Auch hier sind wieder die Stoffmengenanteile der beiden beteiligten Einzelsalze gegeneinander aufgetragen, in diesem Fall bei einer Temperatur von 25 °C (die Phasen Na<sub>2</sub>SO<sub>4</sub>∙10H<sub>2</sub>O und MgSO<sub>4</sub>∙7H<sub>2</sub>O sind darauf zurückzuführen, dass sie bei dieser Temperatur in den jeweiligen Salzsystemen die stabilen Phasen darstellen). Da das Doppelsalz kongruent löslich ist, kristallisiert es aus Lösungen aus, die die gleiche Zusammensetzung haben wie das Salz selbst. Anhand der Summenformel des Salzes kann schon erkannt werden, dass es aus einer äquimolaren Mischung von Natrium- und Magnesiumsulfat auskristallisiert. Diese ist durch die hellgraue Linie im Diagramm dargestellt. Beim Erreichen der Sättigungskonzentration am Punkt A kristallisiert [[Astrakanit | Blödit]] aus, wobei gleiche Mengen Natrium- und Magnesiumsulfat der Lösung entzogen werden. Im Verhältnis verändert sich die Lösungszusammensetzung nicht, so dass nur [[Astrakanit | Blödit]] auskristallisiert und es sich somit wie ein Einzelsalz verhält. Ebenso ist es bei der Betrachtung des Deliqueszenzverhaltens. Liegt reines [[Astrakanit | Blödit]] vor, so beginnt es ab seiner Sättigungsfeuchte Wasserdampf aus der Umgebung aufzunehmen und bildet zunächst eine gesättigt Lösung. Bei weiterem Anstieg der relativen Feuchte löst sich das Salz unter Bildung einer Lösung mit äquimolaren Anteilen Natrium- und Magnesiumsulfat wieder auf <bib id="Steiger.etal:2014"/>. Wird hingegen von einer Mischung mit einem Überschuss an Magnesiumsulfat ausgegangen (Punkt B), so wird bei voranschreitender Verdunstung [[Magnesiumsulfat-Heptahydrat]] bei der entsprechenden Sättigungsfeuchte auskristallisiert (Punkt C). Die Kristallisation schreitet entlang C-D voran. Da im Verhältnis der Stoffmengenanteil von [[Natriumsulfat]] ansteigt, bildet sich [[Astrakanit | Blödit]] an Punkt D (Endpunkt der Kristallisation). | Die Betrachtung von Salzgemischen kann noch weiter ausgeführt werden. In vielen Salzmischungen können sich Doppelsalze bilden, also solche Salze, die drei oder mehr verschiedene Ionen enthalten. Wie bereits oben erwähnt, gibt es sowohl kongruent als auch inkongruent lösliche Doppelsalze. Zunächst soll ein Löslichkeitsdiagramm einer Mischung aus Na<sub>2</sub>SO<sub>4</sub> und MgSO<sub>4</sub> betrachtet werden (Abbildung 9), da sich in einem solchen Gemisch ein kongruent lösliches Doppelsalz ([[Astrakanit]] alias [[Astrakanit | Blödit]]; Na<sub>2</sub>Mg(SO<sub>4</sub>)<sub>2</sub>∙4H<sub>2</sub>O) bilden kann. Auch hier sind wieder die Stoffmengenanteile der beiden beteiligten Einzelsalze gegeneinander aufgetragen, in diesem Fall bei einer Temperatur von 25 °C (die Phasen Na<sub>2</sub>SO<sub>4</sub>∙10H<sub>2</sub>O und MgSO<sub>4</sub>∙7H<sub>2</sub>O sind darauf zurückzuführen, dass sie bei dieser Temperatur in den jeweiligen Salzsystemen die stabilen Phasen darstellen). Da das Doppelsalz kongruent löslich ist, kristallisiert es aus Lösungen aus, die die gleiche Zusammensetzung haben wie das Salz selbst. Anhand der Summenformel des Salzes kann schon erkannt werden, dass es aus einer äquimolaren Mischung von Natrium- und Magnesiumsulfat auskristallisiert. Diese ist durch die hellgraue Linie im Diagramm dargestellt. Beim Erreichen der Sättigungskonzentration am Punkt A kristallisiert [[Astrakanit | Blödit]] aus, wobei gleiche Mengen Natrium- und Magnesiumsulfat der Lösung entzogen werden. Im Verhältnis verändert sich die Lösungszusammensetzung nicht, so dass nur [[Astrakanit | Blödit]] auskristallisiert und es sich somit wie ein Einzelsalz verhält. Ebenso ist es bei der Betrachtung des Deliqueszenzverhaltens. Liegt reines [[Astrakanit | Blödit]] vor, so beginnt es ab seiner Sättigungsfeuchte Wasserdampf aus der Umgebung aufzunehmen und bildet zunächst eine gesättigt Lösung. Bei weiterem Anstieg der relativen Feuchte löst sich das Salz unter Bildung einer Lösung mit äquimolaren Anteilen Natrium- und Magnesiumsulfat wieder auf <bib id="Steiger.etal:2014"/>. Wird hingegen von einer Mischung mit einem Überschuss an Magnesiumsulfat ausgegangen (Punkt B), so wird bei voranschreitender Verdunstung [[Epsomit | Magnesiumsulfat-Heptahydrat]] bei der entsprechenden Sättigungsfeuchte auskristallisiert (Punkt C). Die Kristallisation schreitet entlang C-D voran. Da im Verhältnis der Stoffmengenanteil von [[Natriumsulfat]] ansteigt, bildet sich [[Astrakanit | Blödit]] an Punkt D (Endpunkt der Kristallisation). | ||
[[File:Na2SO4-MgSO4 mix.jpg|400px|thumb|left|'''Abbildung 9''': Löslichkeiten bei 25 °C im System Na<sub>2</sub>SO<sub>4</sub>-MgSO<sub>4</sub>-H<sub>2</sub>O. Aufgetragen ist die Molalität <i>m</i> von MgSO<sub>4</sub> gegen die von Na<sub>2</sub>SO<sub>4</sub> <bib id="Steiger.etal:2014"/>.]] | [[File:Na2SO4-MgSO4 mix.jpg|400px|thumb|left|'''Abbildung 9''': Löslichkeiten bei 25 °C im System Na<sub>2</sub>SO<sub>4</sub>-MgSO<sub>4</sub>-H<sub>2</sub>O. Aufgetragen ist die Molalität <i>m</i> von MgSO<sub>4</sub> gegen die von Na<sub>2</sub>SO<sub>4</sub> <bib id="Steiger.etal:2014"/>.]] | ||
| Zeile 104: | Zeile 104: | ||
<br clear=all> | <br clear=all> | ||
Bislang wurden nur Salzmischungen mit drei verschiedenen Ionen betrachtet. Das Verhalten und auch die Darstellung von Mischungen mit vier verschiedenen Ionen werden dabei deutlich komplizierter. Hinsichtlich der Darstellung wird die Wasserkomponente zum Zweck der Übersichtlichkeit nicht mit dargestellt. Eine solche Darstellung wird auch als Jänecke-Projektion <bib id="Jaenecke:1906"/> bezeichnet. Als Beispiel für ein solches Diagramm soll das eines Gemischs aus Na<sup>+</sup>-K<sup>+</sup>-NO<sub>3</sub><sup>-</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O bei 25 °C aus Abbildung 11 besprochen werden. Auf der y-Achse sind die auf die Ladungsäquivalente bezogenen Molenbrüche der Nitrationen dargestellt, auf der x-Achse die der Kaliumionen. Alle Mischungen werden durch die auf die Ladungsäquivalente bezogenen Molenbrüche dargestellt, da auf diese Weise die Wertigkeit der Ionen berücksichtigt werden kann. Das bedeutet im Falle dieses Diagramms, dass sämtliche Mischungen als Teilbeitrag der Kalium-Kationen beziehungsweise der Nitrat-Anionen zur Gesamtmenge positiver beziehungsweise negativer Ladungen dargestellt werden. Beispielsweise leuchtet ein, dass bei sehr geringen Stoffmengenanteilen an Kalium- und Nitrat-Ionen Natrium- und Sulfat-Ionen überwiegen. Somit liegen in den Ecken die vier reinen Salze vor. Unten links [[Natriumsulfat]], oben links [[Natriumnitrat]], oben rechts [[Kaliumnitrat]] und unten rechts [[Kaliumsulfat]]. Die Felder innerhalb des Diagramms zeigen die Stabilitätsfelder der möglichen Phasen. Sie werden durch Linien getrennt, durch die die Sättigungskonzentrationen von Lösungen angegeben werden, bei denen die jeweils angrenzenden Phasen im Gleichgewicht vorliegen. Das heißt, dass innerhalb eines Feldes nur Sättigung in Bezug auf eine einzige Phase vorliegt, an Schnittpunkten von Sättigungskurven liegen drei Phasen gemeinsam im Gleichgewicht vor. An diesen Schnittpunkten liegen isotherme invariante Phasen vor (Phasenregel) <bib id="Steiger.etal:2014"/>. | Bislang wurden nur Salzmischungen mit drei verschiedenen Ionen betrachtet. Das Verhalten und auch die Darstellung von Mischungen mit vier verschiedenen Ionen werden dabei deutlich komplizierter. Hinsichtlich der Darstellung wird die Wasserkomponente zum Zweck der Übersichtlichkeit nicht mit dargestellt. Eine solche Darstellung wird auch als Jänecke-Projektion <bib id="Jaenecke:1906"/> bezeichnet. Als Beispiel für ein solches Diagramm soll das eines Gemischs aus Na<sup>+</sup>-K<sup>+</sup>-NO<sub>3</sub><sup>-</sup>-SO<sub>4</sub><sup>2-</sup>-H<sub>2</sub>O bei 25 °C aus Abbildung 11 besprochen werden. Auf der y-Achse sind die auf die Ladungsäquivalente bezogenen Molenbrüche der Nitrationen dargestellt, auf der x-Achse die der Kaliumionen. Alle Mischungen werden durch die auf die Ladungsäquivalente bezogenen Molenbrüche dargestellt, da auf diese Weise die Wertigkeit der Ionen berücksichtigt werden kann. Das bedeutet im Falle dieses Diagramms, dass sämtliche Mischungen als Teilbeitrag der Kalium-Kationen beziehungsweise der Nitrat-Anionen zur Gesamtmenge positiver beziehungsweise negativer Ladungen dargestellt werden. Beispielsweise leuchtet ein, dass bei sehr geringen Stoffmengenanteilen an Kalium- und Nitrat-Ionen Natrium- und Sulfat-Ionen überwiegen. Somit liegen in den Ecken die vier reinen Salze vor. Unten links [[Natriumsulfat]], oben links [[Nitronatrit | Natriumnitrat]], oben rechts [[Kaliumnitrat]] und unten rechts [[Arcanit | Kaliumsulfat]]. Die Felder innerhalb des Diagramms zeigen die Stabilitätsfelder der möglichen Phasen. Sie werden durch Linien getrennt, durch die die Sättigungskonzentrationen von Lösungen angegeben werden, bei denen die jeweils angrenzenden Phasen im Gleichgewicht vorliegen. Das heißt, dass innerhalb eines Feldes nur Sättigung in Bezug auf eine einzige Phase vorliegt, an Schnittpunkten von Sättigungskurven liegen drei Phasen gemeinsam im Gleichgewicht vor. An diesen Schnittpunkten liegen isotherme invariante Phasen vor (Phasenregel) <bib id="Steiger.etal:2014"/>. | ||
Als Anwendungsbeispiel soll eine Lösungszusammensetzung von Punkt A betrachtet werden. Dieser liegt im Stabilitätsfeld von [[Glaserit]] (NaK<sub>3</sub>(SO<sub>4</sub>)<sub>2</sub>), so dass diese Phase bei Eindunstung der Lösung zuerst auskristallisieren würde. Durch die Kristallisation verändert sich bei voranschreitender Verdunstung die Lösungszusammensetzung, wobei die beteiligten Ionen proportional zu ihrem Vorkommen im auskristallisierenden Salz der Lösung entzogen werden. Dies erfolgt entlang der Linie A-B. An Punkt B liegt auch Sättigung in Bezug auf [[Thenardit]] vor, so dass die beiden Salze gemeinsam auskristallisieren. Durch weitere Kristallisation der beiden Phasen verändert sich die Lösungszusammensetzung weiter, und zwar entlang der Linie B-C. An diesem Punkt ist auch Sättigung in Bezug auf [[Darapskit]] (Na<sub>3</sub>NO<sub>3</sub>SO<sub>4</sub>∙H<sub>2</sub>O) erreicht. Da es sich bei dem Punkt jedoch um einen invarianten Punkt handelt, liegen nur dort die drei Phasen gemeinsam vor. Beim weiteren Eindunsten der Lösung muss [[Thenardit]] sich auflösen, da sein Stabilitätsfeld beim Verlauf entlang C-D verlassen wird. Endpunkt der Kristallisation ist der invariante Punkt D <bib id="Steiger:2009a"/><bib id="Steiger.etal:2008c"/>. | Als Anwendungsbeispiel soll eine Lösungszusammensetzung von Punkt A betrachtet werden. Dieser liegt im Stabilitätsfeld von [[Glaserit]] (NaK<sub>3</sub>(SO<sub>4</sub>)<sub>2</sub>), so dass diese Phase bei Eindunstung der Lösung zuerst auskristallisieren würde. Durch die Kristallisation verändert sich bei voranschreitender Verdunstung die Lösungszusammensetzung, wobei die beteiligten Ionen proportional zu ihrem Vorkommen im auskristallisierenden Salz der Lösung entzogen werden. Dies erfolgt entlang der Linie A-B. An Punkt B liegt auch Sättigung in Bezug auf [[Thenardit]] vor, so dass die beiden Salze gemeinsam auskristallisieren. Durch weitere Kristallisation der beiden Phasen verändert sich die Lösungszusammensetzung weiter, und zwar entlang der Linie B-C. An diesem Punkt ist auch Sättigung in Bezug auf [[Darapskit]] (Na<sub>3</sub>NO<sub>3</sub>SO<sub>4</sub>∙H<sub>2</sub>O) erreicht. Da es sich bei dem Punkt jedoch um einen invarianten Punkt handelt, liegen nur dort die drei Phasen gemeinsam vor. Beim weiteren Eindunsten der Lösung muss [[Thenardit]] sich auflösen, da sein Stabilitätsfeld beim Verlauf entlang C-D verlassen wird. Endpunkt der Kristallisation ist der invariante Punkt D <bib id="Steiger:2009a"/><bib id="Steiger.etal:2008c"/>. | ||
| Zeile 111: | Zeile 111: | ||
<br clear=all> | <br clear=all> | ||
Aussagekraft haben diese Phasendiagramme neben der Ableitung von Kristallisationsabfolgen aber noch in anderer Hinsicht. Die Größe der Stabilitätsfelder verschiedener Phasen geben Hinweise darüber, wie wahrscheinlich es ist, dass diese Phase aus dem Gemisch auskristallisiert. Je größer das Feld, desto mehr Zusammensetzungen können zur Phasenbildung führen. Außerdem ist es wichtig ableiten zu können, welche Phasen des Gemischs gemeinsam vorliegen können. Nur aneinander grenzende oder durch invariante Punkt verbundene Phasen können gemeinsam auftreten. Somit wäre es in dem besprochenen Beispiel nicht möglich, [[Mirabilit]] zusammen mit [[Kaliumnitrat]] oder [[Kaliumsulfat]] zu identifizieren <bib id="Steiger.etal:2014"/>. | Aussagekraft haben diese Phasendiagramme neben der Ableitung von Kristallisationsabfolgen aber noch in anderer Hinsicht. Die Größe der Stabilitätsfelder verschiedener Phasen geben Hinweise darüber, wie wahrscheinlich es ist, dass diese Phase aus dem Gemisch auskristallisiert. Je größer das Feld, desto mehr Zusammensetzungen können zur Phasenbildung führen. Außerdem ist es wichtig ableiten zu können, welche Phasen des Gemischs gemeinsam vorliegen können. Nur aneinander grenzende oder durch invariante Punkt verbundene Phasen können gemeinsam auftreten. Somit wäre es in dem besprochenen Beispiel nicht möglich, [[Mirabilit]] zusammen mit [[Kaliumnitrat]] oder [[Arcanit | Kaliumsulfat]] zu identifizieren <bib id="Steiger.etal:2014"/>. | ||
==Literatur== | ==Literatur== | ||
Version vom 12. April 2023, 08:57 Uhr
Autor: Amelie Stahlbuhk
zurück zu SalzWiki:Portal
Abstract[Bearbeiten]
Grundlegende Eigenschaften von Salzen und Salzgemischen werden zusammen mit Erläuterungen zu Phasen- und Löslichkeitsdiagrammen beschrieben. Dabei sollen nur Salze berücksichtigt werden, die im Bereich der Salzkristallisation auf Objekten des Kulturguts Relevanz haben.
Salze im Bereich Kulturgut[Bearbeiten]
Salze sind ionische Verbindungen, die aus positiv geladenen (Kationen) und negativ geladenen Ionen (Anionen) aufgebaut sind. Kationen und Anionen können ein- oder mehrfach positiv beziehungsweise negativ geladen sein, in einem Salz müssen diese Ladungen jedoch ausgeglichen sein. Für die im Kulturgut aus porösen, anorganischen Materialien auftretenden Salze sind die Kationen des Natrium, Kaliums, Magnesiums und des Calciums am häufigsten vertreten. Die gängigsten Anionen sind Chlorid, Sulfat, Nitrat und Carbonat. In Abhängigkeit der Umgebungsfaktoren, Eintragungsquellen und Restaurierungsgeschichte der Objekte können auch weitere Ionen vorkommen, beispielsweise Barium oder Ammonium. Zudem kann beispielsweise Acetat, im Falle von in Holzschaukästen oder -schränken gelagerten Objekten, in Verbindung mit einem entsprechenden Kation in Ausblühungen vorkommen, da Essigsäure vom Holz emittiert wird. Bei Objekten aus metallischen Materialien können zusätzliche Kationen eine Rolle spielen . In der folgenden Betrachtung werden diese Fälle zunächst nicht weiter behandelt, sondern ein Fokus auf die am häufigsten auf mineralischen Materialien vorkommenden Salze gelegt.
Unterscheidung Einzel-, Doppel- und Tripelsalze[Bearbeiten]
Eine Unterscheidung von Salzen kann danach erfolgen, wie viele verschiedene Kationen und Anionen im jeweiligen Salz vorkommen. Liegen nur ein Kation und ein Anion vor, wie im Falle von Natriumchlorid (Halit, NaCl), handelt es sich um ein Einzelsalz. Ein Beispiel für ein Doppelsalz wäre Darapskit (Na3(SO4)(NO3)∙H2O) mit zwei verschiedenen Anionen, aber auch Aphthitalit (K3Na(SO4)2) mit zwei verschiedenen Kationen. Eine andere Schreibweise macht den Begriff des Doppelsalzes noch einleuchtender:
Aphthitalit: (K3Na(SO4)2) oder Na2SO4∙3K2SO4. Dabei ist die Summenformel verändert und entspricht nicht mehr der Formeleinheit des Salzes, allerdings wird deutlich, dass zwei Einzelsalze beteiligt sind.
Es sind einige Doppelsalze im Bereich von Salzen auf Bauwerken bekannt, die sich auch unter realen Bedingungen bilden können. Tripelsalze, die der Definition nach aus drei verschiedenen Kationen oder Anionen bestehen, gibt es weitaus weniger.
Bei Doppelsalzen lassen sich kongruent und inkongruent lösliche unterscheiden. Im Falle kongruent löslicher Salze entsteht beim Auflösen des Salzes eine Lösung mit der gleichen Zusammensetzung wie die des Salzes selbst. Bei inkongruent löslichen Salzen kommt es beim Lösen, je nach Konzentration, zur Kristallisation anderer Phasen, so dass die Lösung eine andere Zusammensetzung aufweist als das ursprüngliche Salz selbst. Ebenso kommt es bei der Verdunstung einer Lösung mit der Zusammensetzung eines Doppelsalzes nicht zu dessen Kristallisation, da zunächst Sättigung in Bezug auf eine andere Phase erreicht wird. Die Vorhersage von Kristallisations- oder Auflösungsprozessen im Falle inkongruent löslicher Salze ist somit komplizierter und ohne Informationen über Löslichkeiten im System nicht einfach vorhersehbar.
Löslichkeit von Salzen[Bearbeiten]
Salze haben unterschiedliche Löslichkeiten, die zudem eine Temperaturabhängigkeit aufweisen. Im Falle von salzbelasteten Bauwerken sind die Löslichkeiten der Salze ebenfalls relevant. Es kann beispielsweise abgeleitet werden, wie mobil ein Salz im Mauerwerk ist. Liegt ein Salz mit einer geringen Löslichkeit vor, wird es schnell auskristallisieren, nahe des Ortes, an dem die entsprechenden salzbildenden Ionen zusammentreffen. Wird eine Mauer betrachtet, in der das Grundwasser (und mit ihm verschiedene gelöste Salze) durch Kapillarsog aufsteigt, so können diesbezüglich Fraktionierungen erkannt werden. Gut lösliche Salze verweilen auch bei voranschreitender Verdunstung in Lösung und können gelöst in weitere Höhen transportiert werden, während schlecht lösliche Salze kurz oberhalb des Bodens auskristallisieren, da ihre Löslichkeit schneller erreicht wird [Arnold.etal:1991]Titel: Monitoring Wall Paintings Affected by soluble Salts
Autor / Verfasser: Arnold, Andreas; Zehnder, Konrad .
.
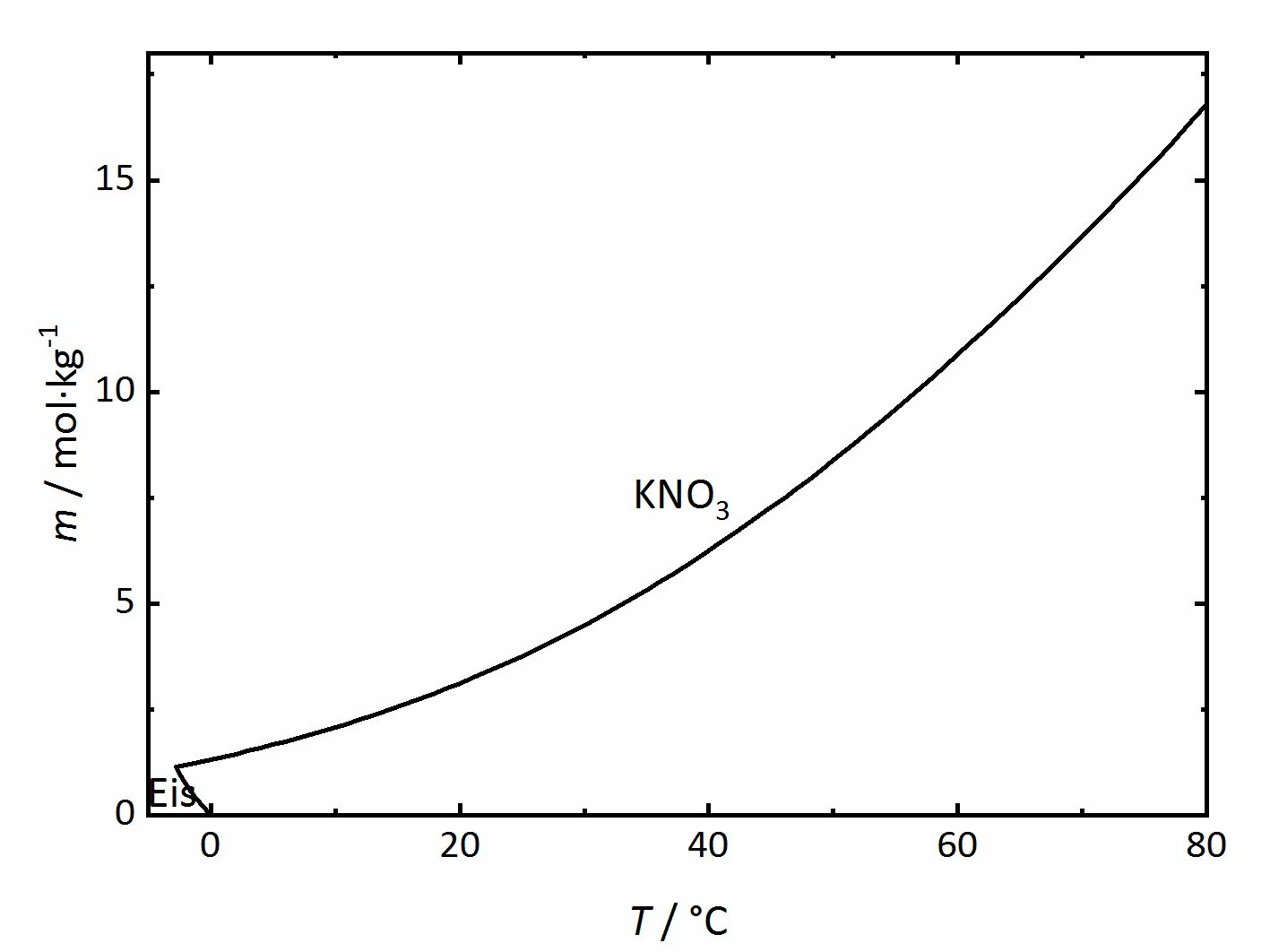
Die Temperaturabhängigkeit der Löslichkeit kann in Löslichkeitsdiagrammen dargestellt werden. Dafür soll zunächst ein simples Löslichkeitsdiagramm eines Einzelsalzes betrachtet werden, beispielsweise von Kaliumnitrat (Abbildung 1). In einem solchen Diagramm ist die Löslichkeit des Salzes in Wasser in Form der Molalität (mol/kgLösungsmittel, das Lösungsmittel ist im Falle der hier betrachteten Lösungen immer Wasser) gegen die Temperatur aufgetragen. Die schwarze Linie im Diagramm gibt die Sättigungskonzentration bei der entsprechenden Temperatur an. Bei 20 °C würde eine Kaliumnitrat-Lösung der Molalität 3.1 mol/kg gesättigt sein. Demnach liegt bei Konzentrationen unterhalb der Linie eine ungesättigte Lösung vor. Oberhalb der Linie liegt eine gesättigte Lösung (bei 20 °C 3.1 mol/kg) mit zunehmender Menge des festen Bodenkörpers vor. Im Falle des Kaliumnitrats nimmt die Löslichkeit mit der Temperatur zu. Bei sehr geringen Temperaturen kommt es zur Bildung von Eis.
Für ein gegebenes Salz kann das Gleichgewicht zwischen Kristallisation und Auflösen durch die folgende allgemeine Gleichung dargestellt werden: Mν,MXν,X•ν0H2O ⇌ νMMzM++νXXzX-+ν0H2O (Gl. 1) Es sind M und X die jeweiligen Kationen und Anionen mit der Anzahl ν und der Ladung z und ν0 die Anzahl möglicher Wassermoleküle, so dass die Gleichung auch für Hydratsalze gilt. Die zugehörige Gleichgewichtskonstante ist das Löslichkeitsprodukt lnKMX. lnKMX=νMlnmM+νXlnmX+νMlnγM+νXlnγX+ν0lnaw (Gl. 2) Es sind m die Molalitäten und γ die Aktivitätskoeffizienten der Kationen und Anionen in einer gesättigten Lösung des Salzes und aw die Wasseraktivität. aw=RH=pw/pw,0 (Gl. 3) Hier sind pw und pw,0 der aktuelle Wasserdampfpartialdruck und der Sättigungspartialdruck, so dass die Wasseraktivität einer sich im Gleichgewicht befindlichen Lösung der relativen Luftfeuchtigkeit über dieser Lösung entspricht.
Hydratsalze[Bearbeiten]
In einer Reihe von Salzsystemen können neben wasserfreien Phasen auch eine oder mehrere Hydratphasen auftreten. Sie zeichnen sich durch in der Kristallstruktur eingebettete Wassermoleküle aus. Mirabilit Na2SO4∙10H2O aus dem System Na+-SO42--H2O enthält demnach pro Formeleinheit zehn Wassermoleküle, gebunden als Kristallwasser, oder anders formuliert kommen auf ein mol Na2SO4 zehn mol H2O. Eine Hydratationsreaktion kann ähnlich wie eine Löslichkeitsreaktion aufgestellt werden:
Mν,MXν,X•ν0,AH2O+(ν0,B-ν0,A)H2O(g) ⇌ Mν,MXν,X•ν0,BH2O (Gl. 4)
Es sind ν0,A und ν0,B die Anzahl der Wassermoleküle in der geringer hydratisierten beziehungsweise der höher hydratisierten Phase. Die Gleichgewichtskonstante für die Hydratationsreaktion KH kann wie folgt formuliert werden:
KH=pw0/pw,AB=1/RHAB (Gl. 5)
Der Sättigungspartialdruck pw0 wird zum Wasserdampfpartialdruck im Gleichgewicht der geringer (A) und der höher (B) hydratisierten Phase pw,AB ins Verhältnis gesetzt, woraus sich der Kehrwert der relativen Luftfeuchtigkeit im Gleichgewicht der beiden Phasen A und B RHAB ergibt. Bei relativen Luftfeuchtigkeiten oberhalb von RHAB findet die Hydratation statt, darunter die Dehydratation [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja [Steiger:2009a]Titel: Modellierung von Phasengleichgewichten
[Steiger:2009a]Titel: Modellierung von Phasengleichgewichten
Autor / Verfasser: Steiger, Michael .
.
Phasendiagramme[Bearbeiten]
In Salzsystemen der Form Mz+-Xz--H2O (M sind die Kationen und X die Anionen, wobei auch mehrere Ionen vorkommen können, und die Ladung z ebenfalls variieren kann) können in Abhängigkeit der Temperatur und der relativen Luftfeuchtigkeit verschiedene Phasen auftreten. In Phasendiagrammen können thermodynamisch stabile Bedingungen für die verschiedenen Phasen abgeleitet werden.
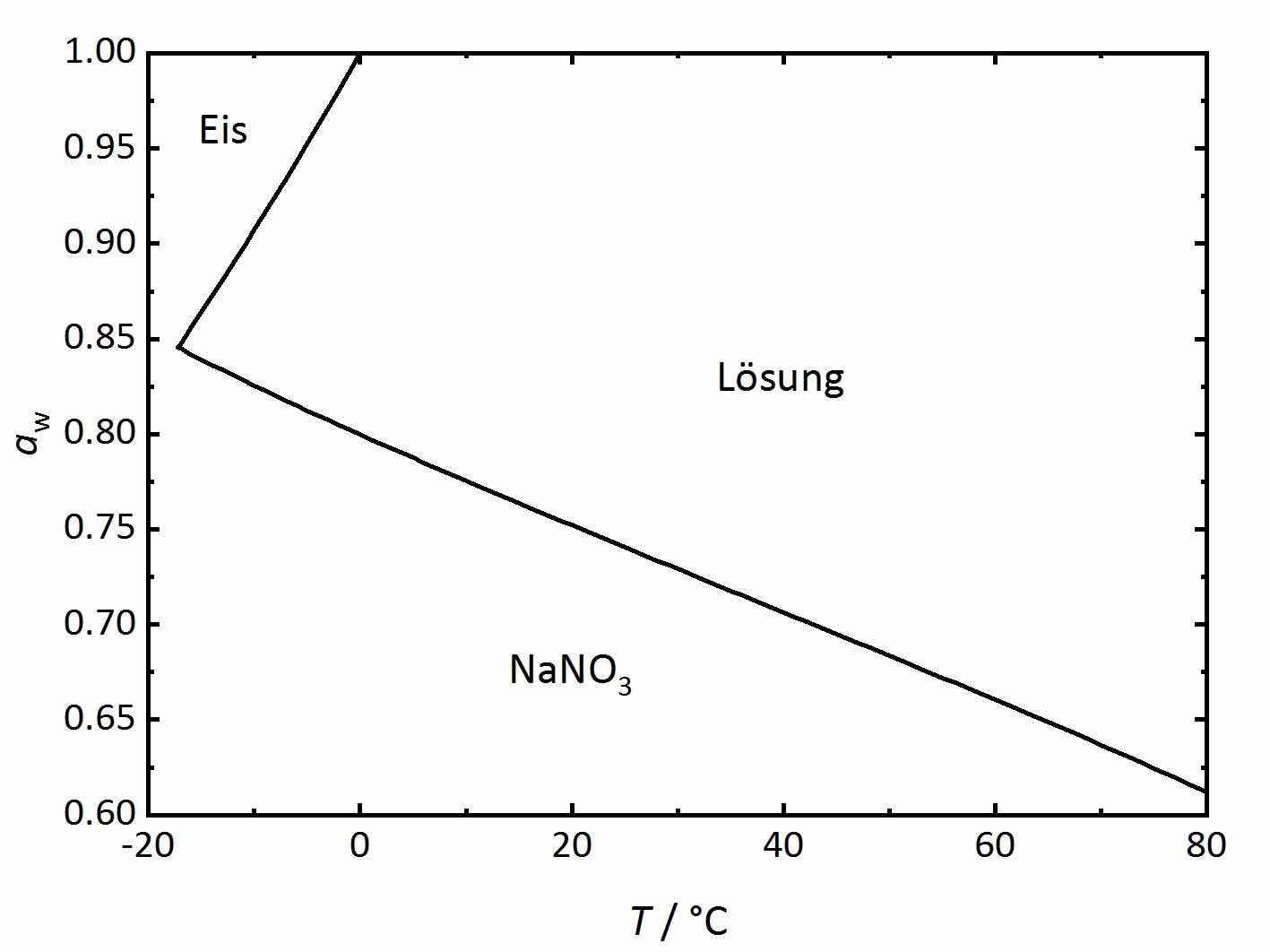
Bei Einzelsalzen, die keine Hydrate bilden, gibt es einen salzspezifischen und temperaturabhängigen Wert der relativen Luftfeuchtigkeit, ab dessen Erreichen das Salz beginnt Wasser in Form von Wasserdampf aus der Umgebung aufzunehmen, um eine gesättigte Lösung zu bilden. Dieser Wert wird als Deliqueszenzfeuchte bezeichnet. An diesem Punkt der gesättigten Lösung liegen die Phasen kristallines Salz, gesättigte Lösung und Wasserdampf der Umgebung im Gleichgewicht vor, so dass die Deliqueszenzfeuchte im Falle von Einzelsalzen der Wasseraktivität der Lösung entspricht. Wird das Phasendiagramm von Natriumnitrat (Abbildung 2) betrachtet, so kann die Deliqueszenzfeuchte bei einer Temperatur von 20 °C anhand der Linie im Diagramm abgelesen werden. Sie liegt demnach bei 75.3 % RH. Im Diagramm kann zudem erkannt werden, dass die Deliqueszenzfeuchte mit zunehmender Temperatur sinkt. Oberhalb der Linie liegt eine Lösung vor, die mit zunehmender relativer Luftfeuchtigkeit bei gegebener Temperatur durch fortschreitende Aufnahme von Wasserdampf aus der Umgebung weiter verdünnt wird. Bei sinkender Feuchte konzentriert sich die Lösung weiter auf, da Wasserdampf an die Umgebung abgegeben wird, bis das Salz bei der Deliqueszenzfeuchte wieder ausfällt und unterhalb dieser nur noch das kristalline Salz vorliegt. Wieviel Wasser oberhalb der Deliqueszenzfeuchte aufgenommen wird, wird durch das Gleichgewicht zwischen Lösung und Wasserdampf der Umgebung, also der gegebenen relativen Luftfeuchtigkeit bestimmt. Herrscht Gleichgewicht, so entspricht die Wasseraktivität der Salzlösung der relativen Feuchte der Umgebung (Gleichung 3). Wird das Gleichgewicht durch Änderung der Feuchte verlassen, wird solange Wasserdampf aus der Umgebung aufgenommen beziehungsweise an sie abgegeben, bis das neue Gleichgewicht erreicht ist.
Autor / Verfasser: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas

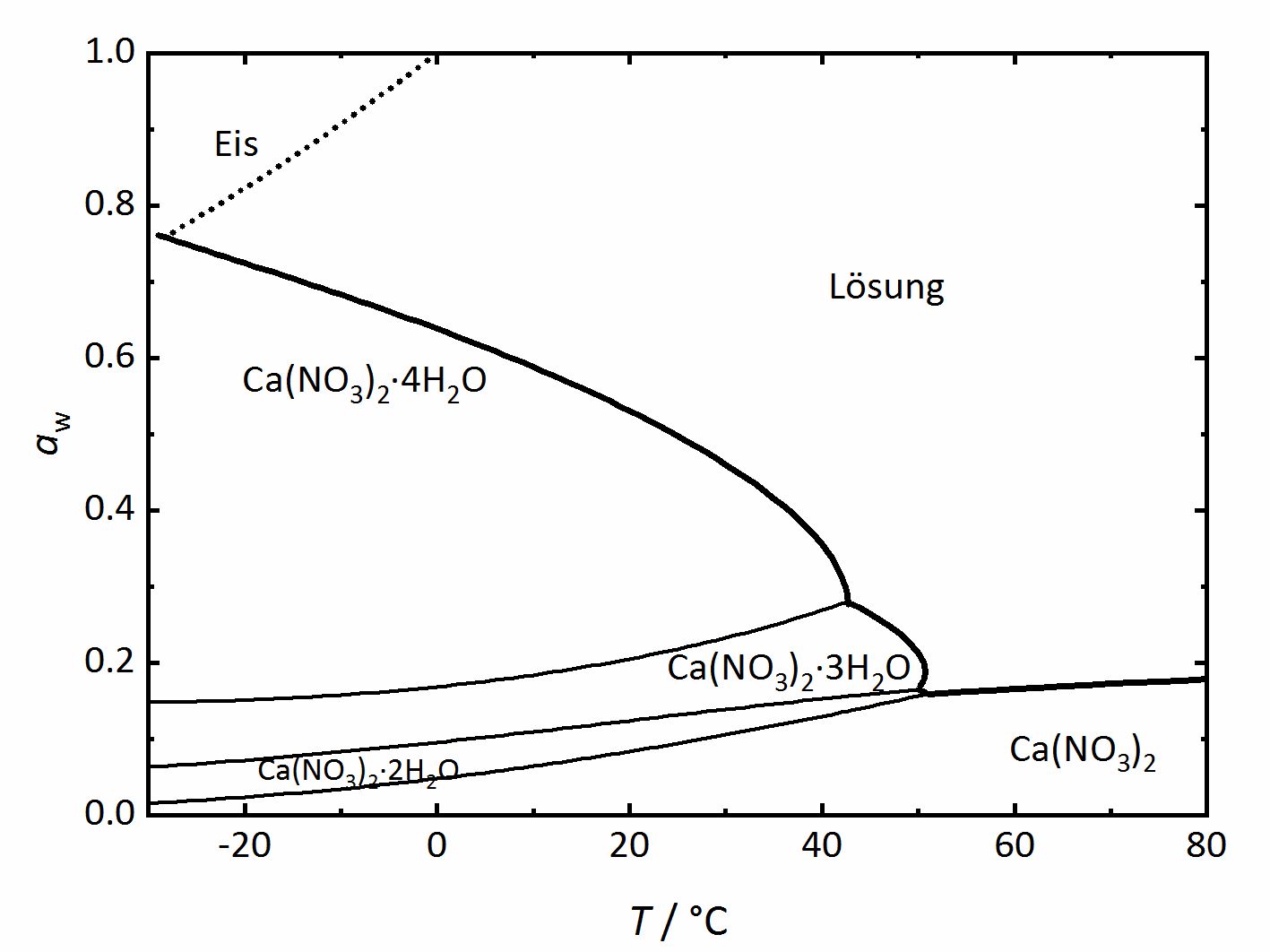
Neben einfachen Einzelsalzen, gibt es auch eine Vielzahl an Salzen, die in verschiedenen Hydratphasen vorliegen. Ein recht einfaches Phasendiagramm für ein Salzsystem mit mehreren möglichen Hydratstufen ist das des Systems Ca2+-NO3--H2O (Abbildung 3). In diesem System können vier verschiedene Hydratstufen auftreten. Ähnlich wie die Deliqueszenzfeuchte den Wert angibt, an dem ein kristallines Salz Wasserdampf aufnimmt und eine gesättigte Lösung bildet, gibt es auch einen Wert der Feuchte, bei dem eine wasserfreie oder geringer hydratisierte Phase Wasserdampf aus der Umgebung aufnimmt, um die höher hydratisierte Phase zu bilden. In einem Phasendiagramm eines Salzsystems mit verschiedenen Hydratstufen gibt es wie auch im Diagramm eines Einzelsalzes Linien für die Deliqueszenzfeuchte, welches die dickeren, am weitesten oben verlaufenden Linien sind. Auch hier beschreibt sie das Gleichgewicht zwischen kristallinem Salz, gesättigter Lösung und Wasserdampf in der Luft. Zusätzlich befinden sich aber noch weitere Linien im Diagramm, die andere Phasenübergänge beschreiben und als dünnere Linien dargestellt sind. Sie repräsentieren Dehydratations- beziehungsweise Hydratationsgleichgewichte zwischen einer geringer und einer höher hydratisierten Phase. Bei Bedingungen, die auf der Linie liegen, liegen beide Phasen gemeinsam vor, darüber die jeweils höher hydratisierte Form, darunter die jeweils geringer hydratisierte Form. Zusätzlich zu den eben genannten Phasenübergängen muss bei sehr geringen Temperaturen auch die Eisbildung berücksichtigt werden, so dass die gepunktete Linie die Gefrierpunkte angibt. Somit kann eine Lösung bei Temperaturen unterhalb von 0 °C sowohl im Gleichgewicht mit Eis als auch mit dem Calciumnitrat-Tetrahydrat (Nitrocalcit) vorliegen [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
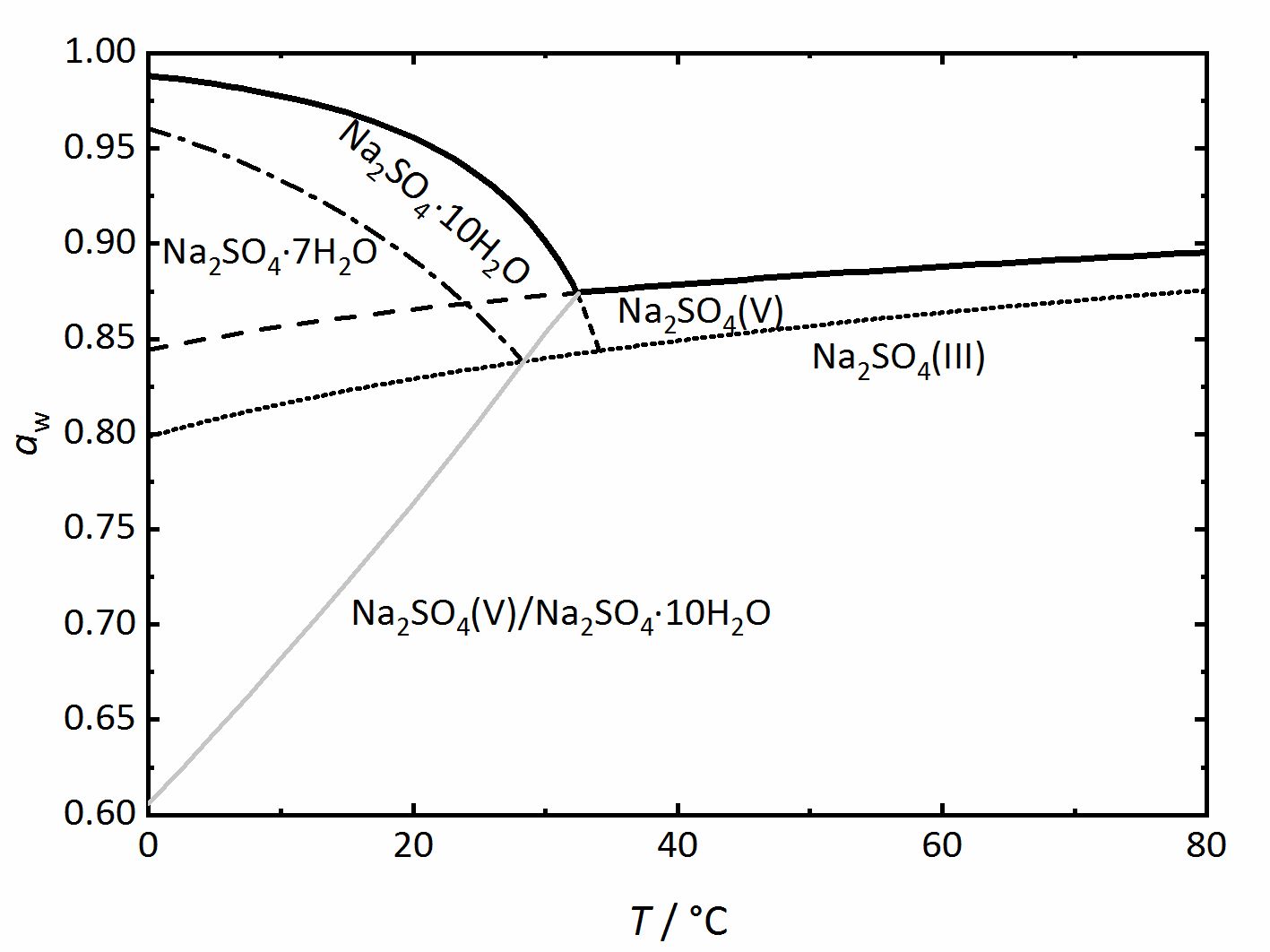
Da die Phasendiagramme von Salzsystemen mit Hydratstufen auch noch komplexer sein können, soll auch auf das System Na+-SO42--H2O [Steiger.etal:2008]Titel: Crystallization of sodium sulfate phases in porous materials: The phase diagram Na2SO4 -H2O and the generation of stress
Autor / Verfasser: Steiger, Michael; Asmussen, Sönke eigegangen werden (Abbildung 4). Auch hier kennzeichnen die am weitesten oben verlaufenden, dickeren Linien das Gleichgewicht zwischen einer gesättigten Lösung und dem kristallinen Salz und somit die Deliqueszenzfeuchte. Die graue Linie repräsentiert das Dehydratations- beziehungsweise das Hydratationsgleichgewicht zwischen der wasserfreien Phase (Thenardit) und dem Decahydrat (Mirabilit). Mirabilit und Thenardit sind nicht bei allen Temperaturen stabil, so dass im Diagramm auch eine Umwandlungstemperatur bei 32.4 °C erkennbar ist. Oberhalb dieser ist Mirabilit keine stabile Phase mehr, darunter ist Thenardit thermodynamisch nicht mehr stabil. Die Linien dieser beiden Salze sind allerdings auch unterhalb (im Falle des Thenardits) beziehungsweise oberhalb (im Falle der Mirabilits) der Umwandlungstemperatur gezeigt, in diesen Bereichen jedoch nur als gestrichelte Linien. Zusätzlich sind weitere gestrichelt beziehungsweise gepunktet dargestellte Linien zu sehen, Phasengrenzen zwischen Natriumsulfat-Heptahydrat beziehungsweise Natriumsulfat Phase III (eine wasserfreie Phase) und den oben bereits erläuterten Phasen. Diese Linien stellen einen Unterschied zu den zuvor vorgestellten Diagrammen dar. Sie repräsentieren metastabile Phasen oder Bereiche. Das bedeutet, dass die Phasen zwar thermodynamisch nicht stabil sind, sie sich aus kinetischen Gründen aber trotzdem bilden können. Bezüglich des Heptahydrats und der Phase III gibt es mehrere Belege, dass sie sich unter bestimmten Bedingungen des Abkühlens oder Eindampfens von Lösungen bilden können, auch wenn Thenardit oder Mirabilit die thermodynamisch stabilen Phasen bilden würden (z.B. [Espinosa.etal:2008]Titel: Model for the mechanical stress due to the salt crystallization in porous materials
eigegangen werden (Abbildung 4). Auch hier kennzeichnen die am weitesten oben verlaufenden, dickeren Linien das Gleichgewicht zwischen einer gesättigten Lösung und dem kristallinen Salz und somit die Deliqueszenzfeuchte. Die graue Linie repräsentiert das Dehydratations- beziehungsweise das Hydratationsgleichgewicht zwischen der wasserfreien Phase (Thenardit) und dem Decahydrat (Mirabilit). Mirabilit und Thenardit sind nicht bei allen Temperaturen stabil, so dass im Diagramm auch eine Umwandlungstemperatur bei 32.4 °C erkennbar ist. Oberhalb dieser ist Mirabilit keine stabile Phase mehr, darunter ist Thenardit thermodynamisch nicht mehr stabil. Die Linien dieser beiden Salze sind allerdings auch unterhalb (im Falle des Thenardits) beziehungsweise oberhalb (im Falle der Mirabilits) der Umwandlungstemperatur gezeigt, in diesen Bereichen jedoch nur als gestrichelte Linien. Zusätzlich sind weitere gestrichelt beziehungsweise gepunktet dargestellte Linien zu sehen, Phasengrenzen zwischen Natriumsulfat-Heptahydrat beziehungsweise Natriumsulfat Phase III (eine wasserfreie Phase) und den oben bereits erläuterten Phasen. Diese Linien stellen einen Unterschied zu den zuvor vorgestellten Diagrammen dar. Sie repräsentieren metastabile Phasen oder Bereiche. Das bedeutet, dass die Phasen zwar thermodynamisch nicht stabil sind, sie sich aus kinetischen Gründen aber trotzdem bilden können. Bezüglich des Heptahydrats und der Phase III gibt es mehrere Belege, dass sie sich unter bestimmten Bedingungen des Abkühlens oder Eindampfens von Lösungen bilden können, auch wenn Thenardit oder Mirabilit die thermodynamisch stabilen Phasen bilden würden (z.B. [Espinosa.etal:2008]Titel: Model for the mechanical stress due to the salt crystallization in porous materials
Autor / Verfasser: Espinosa, R.; Franke, L.; Deckelmann, G. [Genkinger.etal:2007]Titel: Crystallisation of sodium sulfate: supersaturation and metastable phases
[Genkinger.etal:2007]Titel: Crystallisation of sodium sulfate: supersaturation and metastable phases
Autor / Verfasser: Genkinger, Selma; Putnis, Andrew [Grossi.etal:2013]Titel: Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones
[Grossi.etal:2013]Titel: Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones
Autor / Verfasser: Grossi, C.M.; Esbert, R.M.; Suarez del Rio, L.M.; Montoto, M.; Laurenzi-Tabasso, M. [Linnow.etal:2006]Titel: Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction
[Linnow.etal:2006]Titel: Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction
Autor / Verfasser: Linnow, Kirsten; Zeunert, Anke; Steiger, Michael [Xu.etal:1999]Titel: In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.
[Xu.etal:1999]Titel: In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.
Autor / Verfasser: Xu B., Schweiger G. ). Metastabile Phasen sind somit auch unter realen Bedingungen relevant und sollten nicht vernachlässigt werden.
). Metastabile Phasen sind somit auch unter realen Bedingungen relevant und sollten nicht vernachlässigt werden.
Autor / Verfasser: Steiger, Michael; Asmussen, Sönke

In Bezug auf stark hygroskopische Salze wie Calciumnitrat oder Calciumchlorid liegen in den Phasendiagrammen zwar keine Phasengrenzen für mögliche metastabile Phasen vor, jedoch sind metastabile Zustände bei diesen Salzen trotzdem relevant. Die Phasengrenze des Gleichgewichts zwischen Lösung und kristallinem Salz gibt zwar aus thermodynamischer Sicht den Punkt an, bei dem das Salz auskristallisieren müsste, um eine gesättigte Lösung zu bilden. Da einige dieser Salzlösungen jedoch teilweise stark übersättigen können, kann die Lösung auch unterhalb der Deliqueszenzfeuchte als metastabiler Zustand vorliegen [Steiger:2009a]Titel: Modellierung von Phasengleichgewichten
Autor / Verfasser: Steiger, Michael .
.
Salzmischungen[Bearbeiten]
In den meisten realen Objekten des kulturellen Erbes liegen Gemische mehrerer Ionen und somit auch mehrerer Salze vor, wodurch ihre Betrachtung komplizierter wird. Eine Vorhersage über ihr Verhalten unter bestimmten klimatischen Bedingungen ist nicht mehr so einfach möglich wie für Einzelsalze, bei denen Werte für die Deliqueszenzfeuchte und Hydratationsgleichgewichte aus den Phasendiagrammen abgelesen werden können. Die verschiedenen Salze im Gemisch beeinflussen sich im Hinblick auf ihre Löslichkeiten gegenseitig, so dass Charakteristika wie die Sättigungsfeuchten der Einzelsalze nicht mehr gegeben sind. Somit kann dann bei einer gegebenen Temperatur beispielsweise nicht mehr anhand eines spezifischen Werts abgelesen werden, ab wann das Salz Wasserdampf aus der Umgebung aufnimmt. Bei Salzmischungen muss ein Bereich der klimatischen Bedingungen berücksichtigt werden, in welchem verschiedene Phasen aus dem Gemisch auskristallisieren können. Der Einfluss weiterer Salze auf ein vorliegendes Salz der Form Mν,MXν,X∙nH2O kann anhand des thermodynamischen Löslichkeitsprodukts (Gleichung 2) verdeutlicht werden:
Durch ein weiteres Salz wird die Löslichkeit sowohl beeinflusst, wenn ein gleichioniger Zusatz vorliegt (dann wird mM beziehungsweise mX verändert), als auch wenn dies nicht zutrifft (dann werden trotzdem γM und γX beeinflusst) [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Im Folgenden soll je ein Beispiel für einen gleich- und einen fremdionigen Zusatz gezeigt werden.
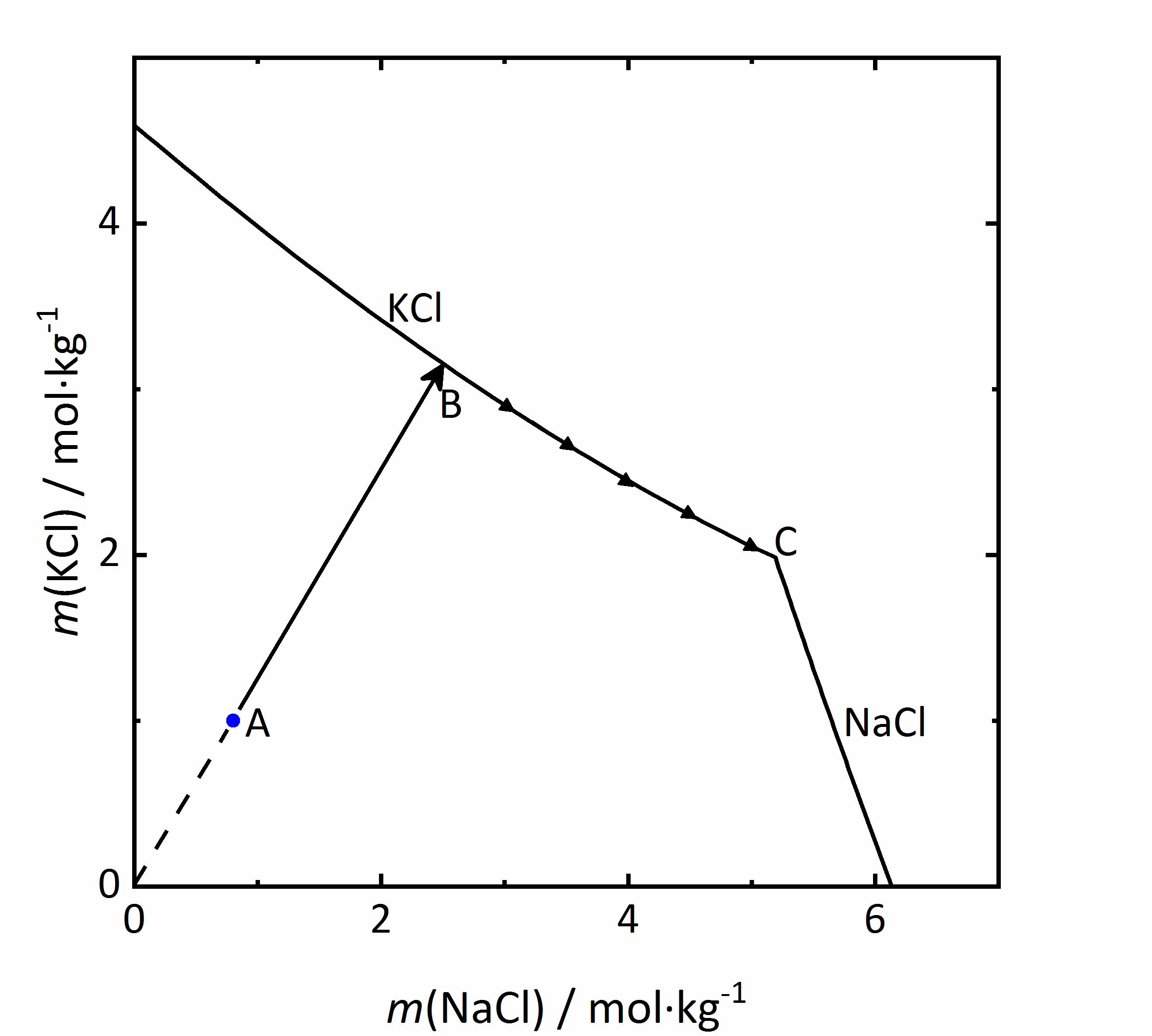
Als Beispiel für einen gleichionigen Zusatz soll das System KCl-NaCl-H2O betrachtet werden. Im Diagramm in Abbildung 5 sind die Molalitäten von KCl gegen die von NaCl aufgetragen. Durch das Vorliegen von Chlorid-Ionen in beiden Salzen, wird mX der Salze (s. Gleichung 1) beeinflusst. Steigt die Konzentration des jeweils anderen Salzes und damit die Chlorid-Konzentration im Gemisch, so nimmt die Löslichkeit des betrachteten Salzes ab. Wird eine Lösung der Zusammensetzung des Punktes A im Diagramm betrachtet, so würde sich die Lösung bei der Verdunstung von Wasserdampf aus der Lösung entlang der Linie AB aufkonzentrieren. An Punkt B wäre Sättigung in Bezug auf KCl erreicht, so dass zunächst dieses Salz aus dem Gemisch auskristallisiert. Da sich die Lösungszusammensetzung durch weitere Verdunstung und durch die Kristallisation von Kaliumchlorid weiter verändert, ist der Kristallisationsverlauf am Punkt B noch nicht abgeschlossen. Im Folgenden kristallisiert KCl entlang seiner Löslichkeitskurve weiter aus, wodurch die Kaliumkonzentration abnimmt, Natriumchlorid sich aber durch die weitere Verdunstung weiter aufkonzentriert. Der Endpunkt C der Kristallisation ist erreicht, wenn Sättigung auch in Bezug auf NaCl erreicht ist, so dass eine dann fortschreitende Verdunstung zur vollständigen Trocknung und Kristallisation beider Phasen führen würde [Steiger:2009a]Titel: Modellierung von Phasengleichgewichten
Autor / Verfasser: Steiger, Michael .
.
Autor / Verfasser: Steiger, Michael
 .
.
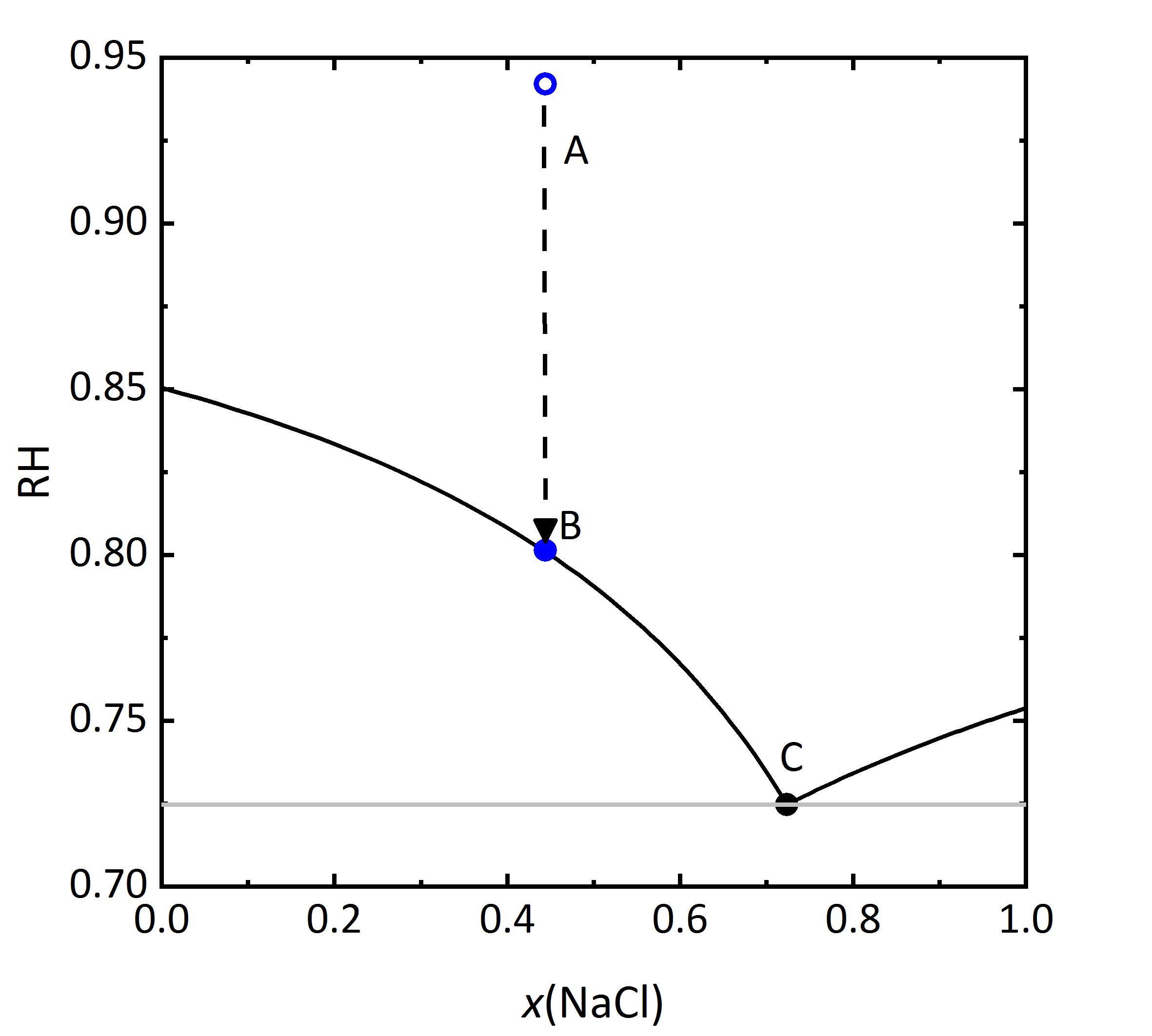
Dass in Salzmischungen auch die Sättigungsfeuchten beeinflusst werden, zeigt das folgende Diagramm in Abbildung 6, in dem die Gleichgewichtsfeuchten der jeweiligen gesättigten Lösungen gezeigt sind. In dem Diagramm ist die relative Luftfeuchtigkeit gegen die Lösungszusammensetzung aufgetragen. Die Lösungszusammensetzung wiederum wird in diesem Falle als Stoffmengenanteil der Natriumchlorid-Konzentration angegeben. Als Stoffmengenanteil wird die Menge einer Komponente des Gemischs in Mol in Bezug auf die Gesamtmenge aller Komponenten bezeichnet. Bei kleinen Stoffmengenanteilen überwiegt demnach Kaliumchlorid in dem Gemisch, bei einem Anteil von 0.5 liegen gleiche molale Mengen Kalium- und Natriumchlorid vor. Wird auch bei diesem Diagramm die Mischung der Zusammensetzung A betrachtet, entspricht die relative Feuchte, die mit dieser Lösung im Gleichgewicht steht 94.2 % RH. Verdunstet Wasser aus der Lösung, wird bei Punkt B Sättigung in Bezug auf KCl erreicht, die relative Luftfeuchtigkeit, die an diesem Punkt mit der gesättigten Lösung und dem kristallinen Salz im Gleichgewicht steht, beträgt 80.1 % RH. Die eigentliche Deliqueszenzfeuchte von KCl beträgt bei 20 °C 85 % RH, so dass die Kristallisation im Gemisch erst bei niedrigeren Feuchten einsetzt. Diese kann auch wie bei der zur Lösung gehörenden Feuchte als Gleichgewichtsfeuchte bezeichnet werden, aber auch als Sättigungsfeuchte des Punktes B. Wird die relative Luftfeuchte weiter gesenkt, kommt es bei 72.5 % RH zum Kristallisationsendpunkt. Wird im Vergleich zu den Punkten A, B und C auf analoge Weise von einem Punkt der Lösungszusammensetzung bei Stoffmengenanteilen >0.73 von Natriumchlorid ausgegangen, zeigt sich, dass auch in diesem Fall die Kristallisation von zuerst gebildetem Natriumchlorid bei geringerer Luftfeuchtigkeit erfolgt als es die Deliqueszenzfeuchte des Einzelsalzes vermuten lassen würde. Das Diagramm verdeutlich auch, dass ein einzelner (kritischer) Wert, bei dem die Kristallisation des Salzes erfolgt, im Falle von Gemischen nicht ausreichend ist. Hier muss vielmehr ein Bereich der relativen Feuchte betrachtet werden, in welchem die Kristallisation kontinuierlich voranschreitet [Steiger.etal:1996]Titel: Crystallization properties of salt mixtures: comparison of experimental results and model calculations
Autor / Verfasser: Steiger, M.; Zeunert, A. [Price.etal:1994]Titel: Preventing salt damage in porous materials
[Price.etal:1994]Titel: Preventing salt damage in porous materials
Autor / Verfasser: Price, Clifford A.; Brimblecomb, Peter [Steiger.etal:1995]Titel: Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen
[Steiger.etal:1995]Titel: Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen
Autor / Verfasser: Steiger, Michael; Dannecker, Walter . Die obere Grenze des Bereichs der relativen Feuchte wird durch die ursprüngliche Zusammensetzung des Gemischs bestimmt. Die untere Grenze der relativen Feuchte liegt am Kristallisationsendpunkt vor, an dem beide Phasen in fester Form gemeinsam existieren. Der Wert der unteren Grenze wird auch als gemeinsame Deliqueszenzfeuchte (engl.: mutual deliquescence humidity; MDRH) beschrieben, da sie den Wert der relativen Feuchte angibt, bei der eine gemischte Lösung im Gleichgewicht mit den weiteren kristallinen Salzen des Gemischs vorliegen kann [Steiger.etal:2014]Titel: Weathering and Deterioration
. Die obere Grenze des Bereichs der relativen Feuchte wird durch die ursprüngliche Zusammensetzung des Gemischs bestimmt. Die untere Grenze der relativen Feuchte liegt am Kristallisationsendpunkt vor, an dem beide Phasen in fester Form gemeinsam existieren. Der Wert der unteren Grenze wird auch als gemeinsame Deliqueszenzfeuchte (engl.: mutual deliquescence humidity; MDRH) beschrieben, da sie den Wert der relativen Feuchte angibt, bei der eine gemischte Lösung im Gleichgewicht mit den weiteren kristallinen Salzen des Gemischs vorliegen kann [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
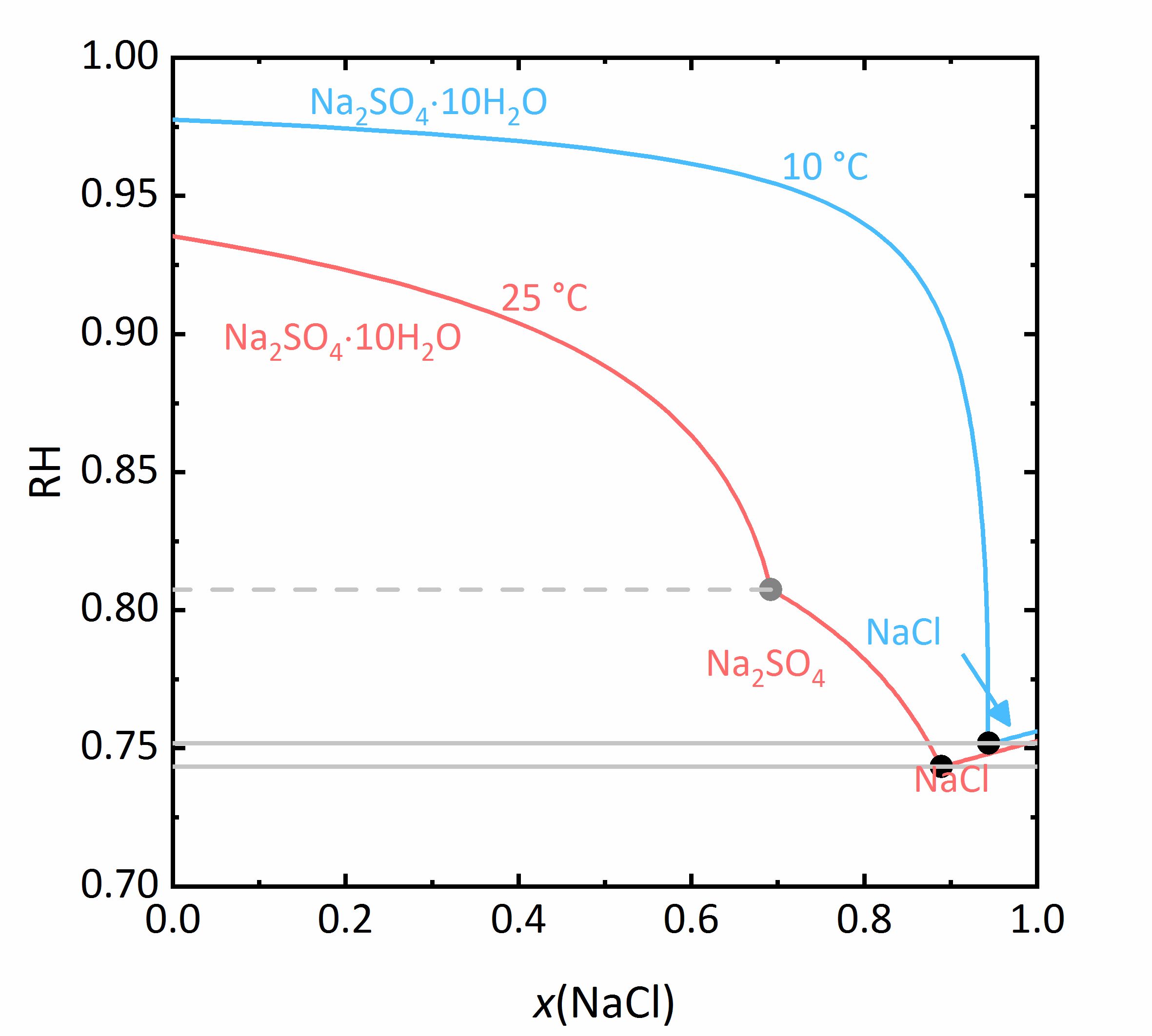
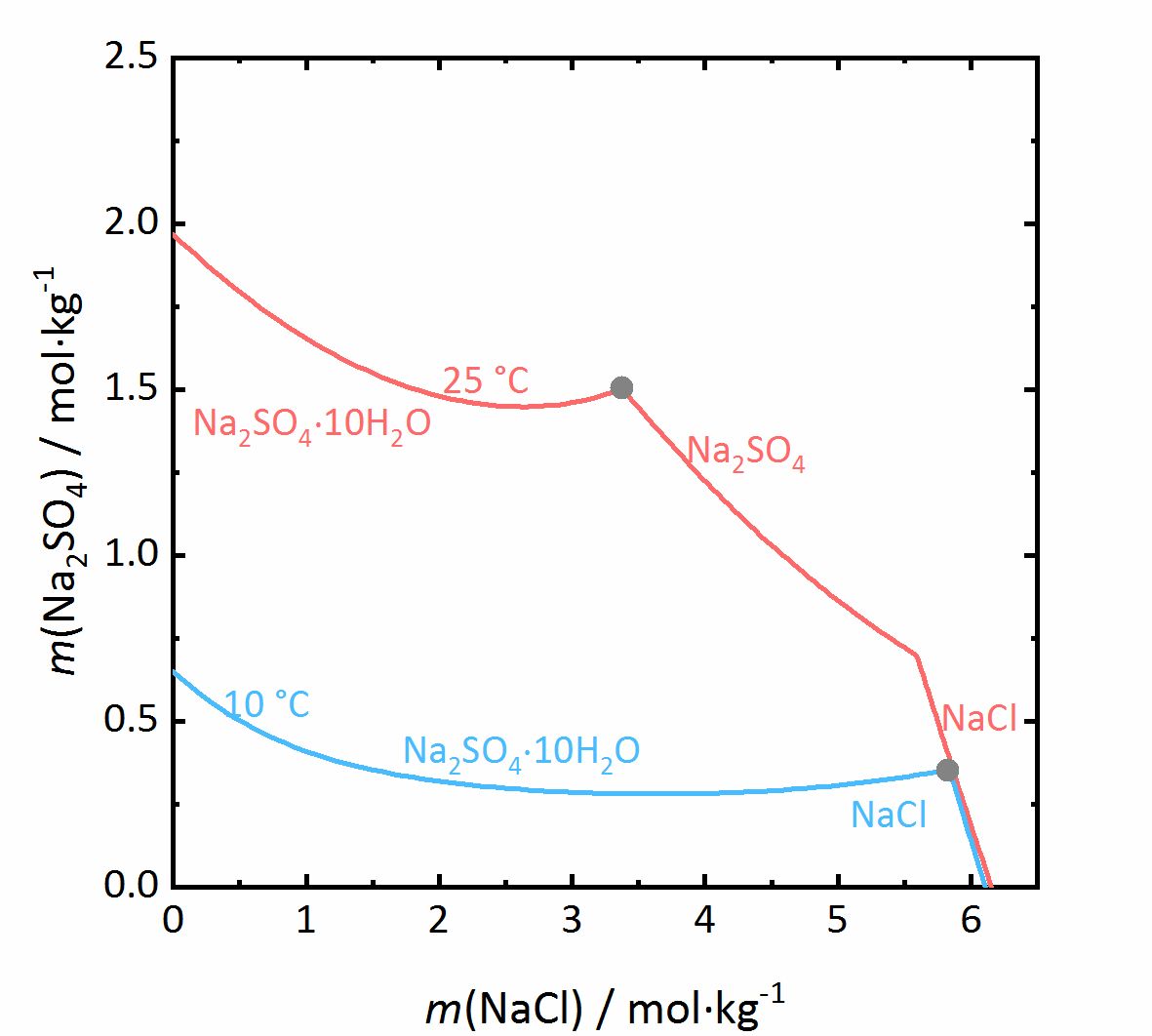
In dem nächsten Beispiel wird das Verhalten der Salzmischungen noch etwas komplizierter. Liegen in einem Gemisch auch Salze vor, die in verschiedenen Hydratstufen vorkommen können, wird nicht nur der Aktivitätskoeffizient beeinflusst, sondern auch die Wasseraktivität. Bei dem Gemisch NaCl-Na2SO4-H2O in Abbildung 7 nimmt die Löslichkeit von Mirabilit trotz eines gleichionigen Zusatzes bei hohen Konzentrationen von Natriumchlorid nochmal zu. Da die Wasseraktivität der Lösung bei steigender Konzentration (also Verdunstung von Wasser) sinkt, erhöht sich die Löslichkeit der Hydratsalze nach einem vorübergehenden Abfall, was am Beispiel des Löslichkeitsdiagramms bei 10 °C verdeutlicht wird. Da das Thenardit-Mirabilit-Dehydratationsgleichgewicht stark temperaturabhängig ist und zudem auch von der Wasseraktivität abhängt, gilt dieses Verhalten jedoch nur bei Temperaturen unterhalb von 18 °C. Liegen höhere Temperaturen vor, so kommt es bei der Kristallisation aus einer solchen gemischten Salzlösung zur Dehydratation des Mirabilits. Unterhalb dieser Temperatur kann die Umwandlung nicht erfolgen, da die relative Feuchte für die Dehydratation (graue Linie im Phasendiagramm von Na2SO4 in Abbildung 4, für die Mischung bei 25 °C graue gestrichelte Linie in Abbildung 8) dann unterhalb der Deliqueszenzfeuchte des Gemischs (jeweils graue Linien in Abbildung 8) liegt. Erst wenn die Gleichgewichtsfeuchte der Umwandlung die Deliqueszenzfeuchte übertrifft, kann Dehydration oder Hydratation in Gegenwart einer Lösung erfolgen. Durch den Zusammenhang der Wasseraktivität mit dem Dehydratationsgleichgewicht kann die Dehydratation von Mirabilit bei Anwesenheit anderer Salze schon bei niedrigeren Temperaturen stattfinden, bei denen Thenardit im reinen Na+-SO42--H2O System im Beisein einer Lösung thermodynamisch nicht stabil wäre. Für reale Objekte kann dies einen wichtiger Aspekt darstellen, da die Hydratation in Anwesenheit einer Lösung weniger erschwert wird. Dadurch können Hydratationsreaktionen schneller ausgelöst werden als bei einer Hydratation ausgelöst durch Wasserdampf, wodurch mögliche Schädigungen des Materials verstärkt werden können. Eine solche Gefahr liegt besonders dann vor, je hygroskopischer das weitere Salz im Gemisch ist, da die Deliqueszenzfeuchte des Gemischs dann geringere Werte annimmt, und die Gleichgewichtsfeuchte der Mirabilit-Thenardit-Umwandlung häufiger darüber liegt. Zu beachten ist, dass die Werte der Gleichgewichtsfeuchte für die Umwandlung durch andere Salze nicht beeinflusst werden. Ausschlaggebend ist lediglich, ob die Werte der Umwandlung oberhalb oder unterhalb der Deliqueszenzfeuchte des Gemischs liegen [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
Salzgemische, in denen Doppelsalze gebildet werden können[Bearbeiten]
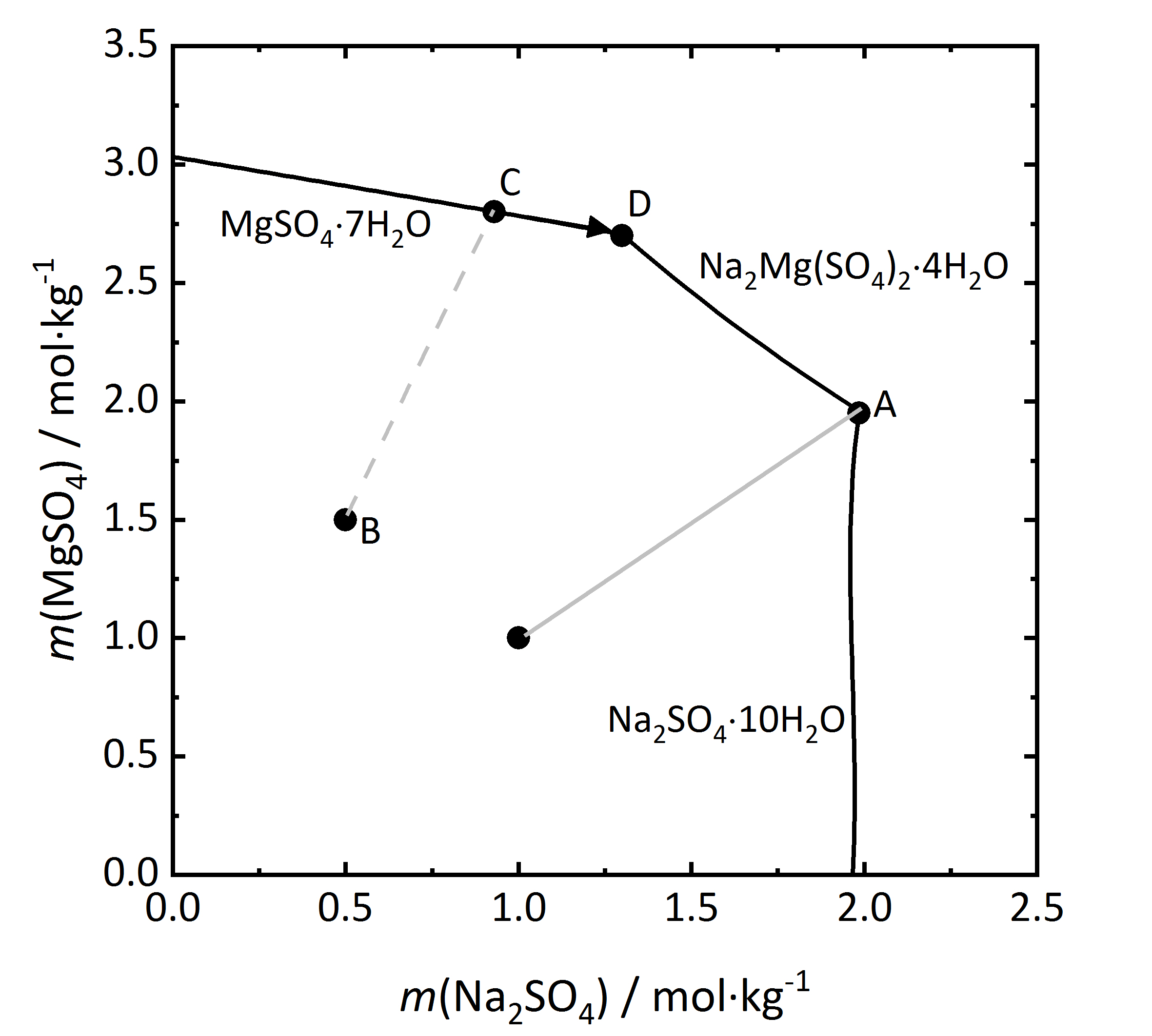
Die Betrachtung von Salzgemischen kann noch weiter ausgeführt werden. In vielen Salzmischungen können sich Doppelsalze bilden, also solche Salze, die drei oder mehr verschiedene Ionen enthalten. Wie bereits oben erwähnt, gibt es sowohl kongruent als auch inkongruent lösliche Doppelsalze. Zunächst soll ein Löslichkeitsdiagramm einer Mischung aus Na2SO4 und MgSO4 betrachtet werden (Abbildung 9), da sich in einem solchen Gemisch ein kongruent lösliches Doppelsalz (Astrakanit alias Blödit; Na2Mg(SO4)2∙4H2O) bilden kann. Auch hier sind wieder die Stoffmengenanteile der beiden beteiligten Einzelsalze gegeneinander aufgetragen, in diesem Fall bei einer Temperatur von 25 °C (die Phasen Na2SO4∙10H2O und MgSO4∙7H2O sind darauf zurückzuführen, dass sie bei dieser Temperatur in den jeweiligen Salzsystemen die stabilen Phasen darstellen). Da das Doppelsalz kongruent löslich ist, kristallisiert es aus Lösungen aus, die die gleiche Zusammensetzung haben wie das Salz selbst. Anhand der Summenformel des Salzes kann schon erkannt werden, dass es aus einer äquimolaren Mischung von Natrium- und Magnesiumsulfat auskristallisiert. Diese ist durch die hellgraue Linie im Diagramm dargestellt. Beim Erreichen der Sättigungskonzentration am Punkt A kristallisiert Blödit aus, wobei gleiche Mengen Natrium- und Magnesiumsulfat der Lösung entzogen werden. Im Verhältnis verändert sich die Lösungszusammensetzung nicht, so dass nur Blödit auskristallisiert und es sich somit wie ein Einzelsalz verhält. Ebenso ist es bei der Betrachtung des Deliqueszenzverhaltens. Liegt reines Blödit vor, so beginnt es ab seiner Sättigungsfeuchte Wasserdampf aus der Umgebung aufzunehmen und bildet zunächst eine gesättigt Lösung. Bei weiterem Anstieg der relativen Feuchte löst sich das Salz unter Bildung einer Lösung mit äquimolaren Anteilen Natrium- und Magnesiumsulfat wieder auf [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja . Wird hingegen von einer Mischung mit einem Überschuss an Magnesiumsulfat ausgegangen (Punkt B), so wird bei voranschreitender Verdunstung Magnesiumsulfat-Heptahydrat bei der entsprechenden Sättigungsfeuchte auskristallisiert (Punkt C). Die Kristallisation schreitet entlang C-D voran. Da im Verhältnis der Stoffmengenanteil von Natriumsulfat ansteigt, bildet sich Blödit an Punkt D (Endpunkt der Kristallisation).
. Wird hingegen von einer Mischung mit einem Überschuss an Magnesiumsulfat ausgegangen (Punkt B), so wird bei voranschreitender Verdunstung Magnesiumsulfat-Heptahydrat bei der entsprechenden Sättigungsfeuchte auskristallisiert (Punkt C). Die Kristallisation schreitet entlang C-D voran. Da im Verhältnis der Stoffmengenanteil von Natriumsulfat ansteigt, bildet sich Blödit an Punkt D (Endpunkt der Kristallisation).
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
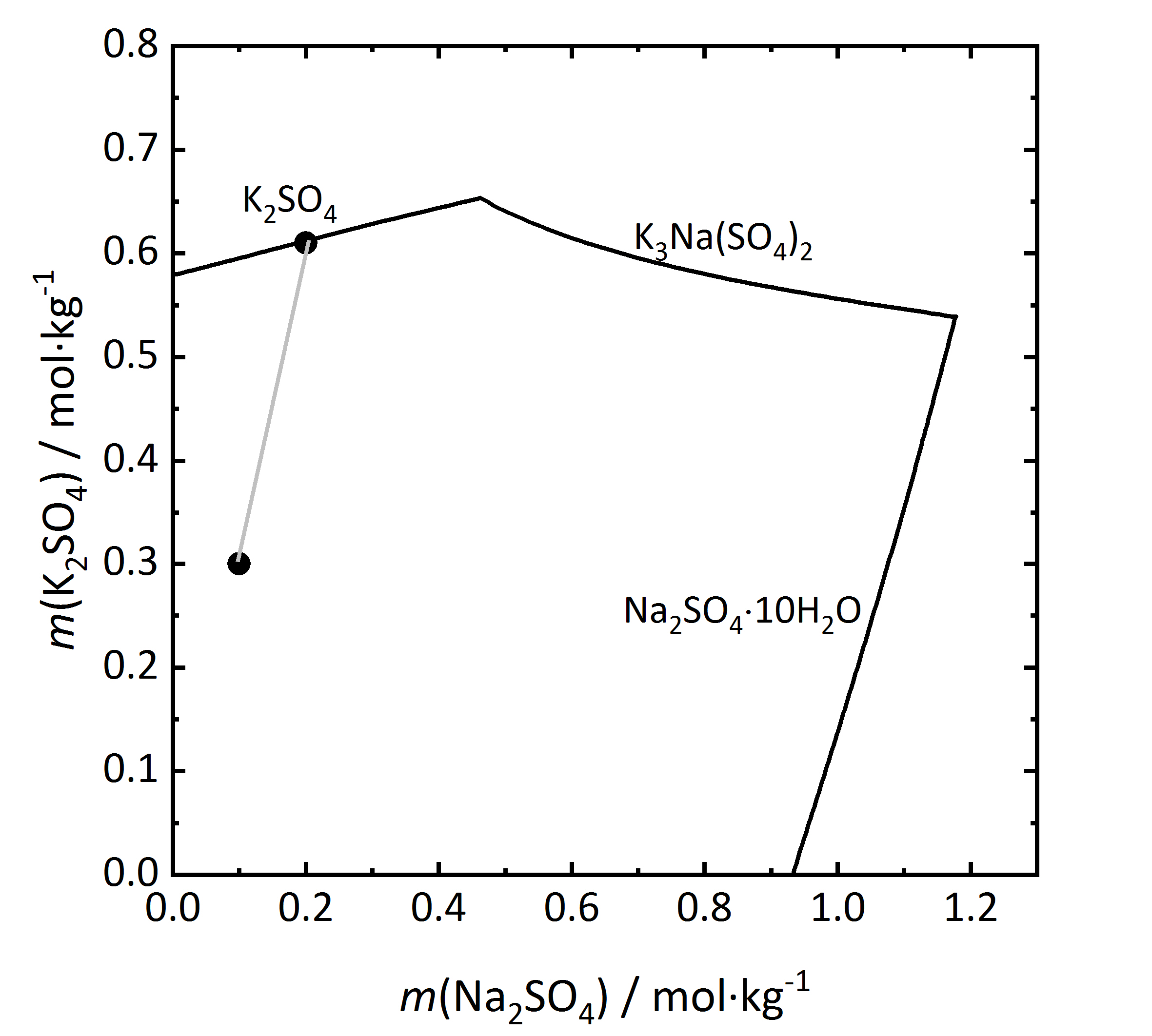
Als nächster Schritt soll in Abbildung 10 ein Löslichkeitsdiragramm eines inkongruent löslichen Doppelsalzes betrachtet werden. Aphthitalit (K3Na(SO4)2) besteht der Summenformel nach aus einer 3:1-Mischung (bezogen auf die Molalität) aus Kalium- und Natriumsulfat. Wird die Verdunstung einer Lösung mit einer solchen Zusammensetzung der Salze verfolgt (bei 15 °C), wird ersichtlich, dass Kaliumsulfat (Arcanit) auskristallisiert, jedoch nicht Aphthitalit. Es ergibt sich, dass eine in Bezug auf das Doppelsalz gesättigte Lösung in Bezug auf Arcanit übersättigt ist. Demnach würde es bei der Auflösung von Aphthitalit in Wasser nicht einfach zur Bildung einer gesättigten Lösung kommen, da Arcanit aufgrund der Übersättigung auskristallisieren würde [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja
 .
.
Bislang wurden nur Salzmischungen mit drei verschiedenen Ionen betrachtet. Das Verhalten und auch die Darstellung von Mischungen mit vier verschiedenen Ionen werden dabei deutlich komplizierter. Hinsichtlich der Darstellung wird die Wasserkomponente zum Zweck der Übersichtlichkeit nicht mit dargestellt. Eine solche Darstellung wird auch als Jänecke-Projektion [Jaenecke:1906]Titel: Über eine neue Darstellungsform der wässerigen Lösungen zweier und dreier gleichioniger Salze, reziproker Salzpaare und der van't Hoffschen Untersuchungen über ozeanische Salzablagerungen.
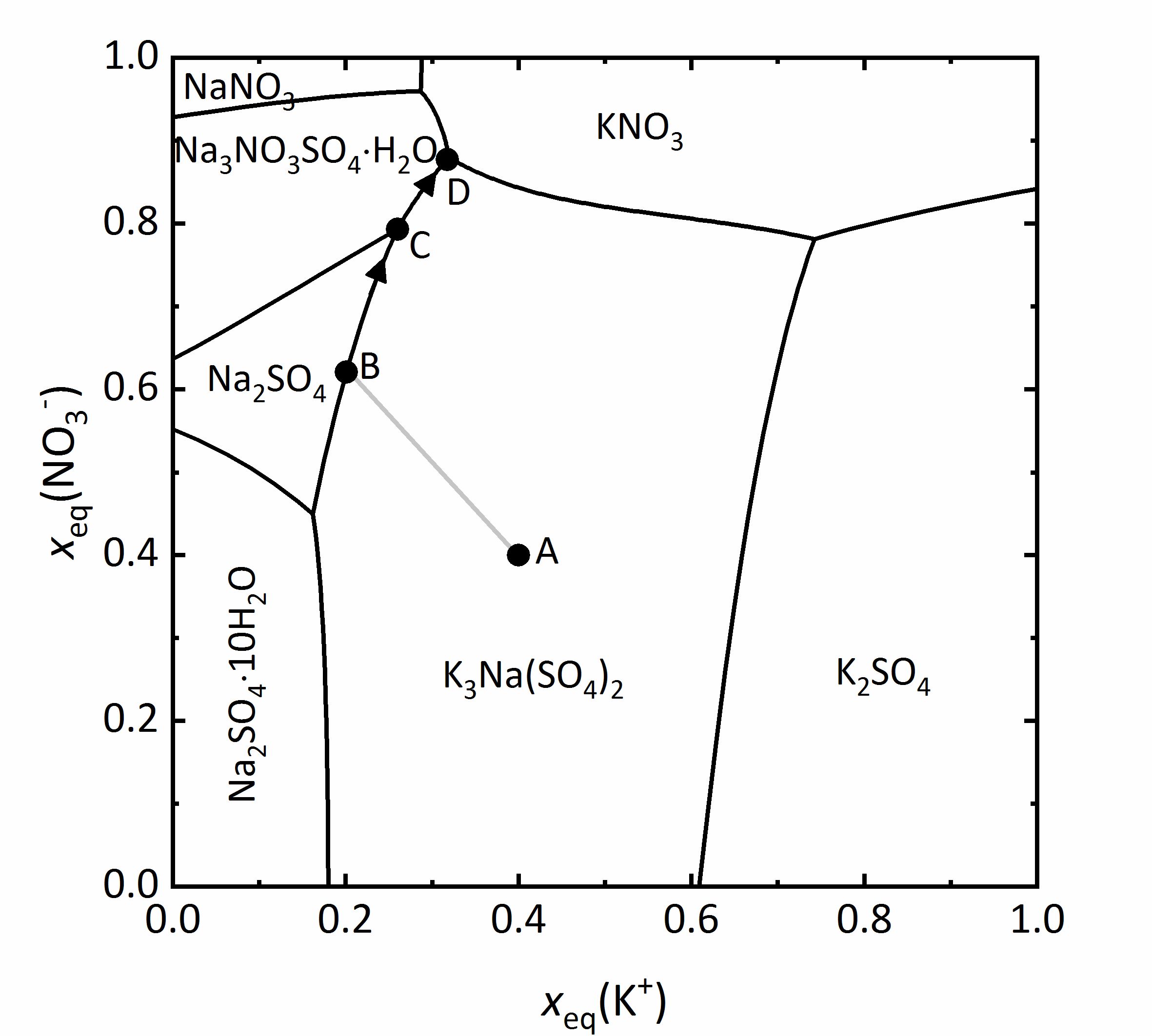
Autor / Verfasser: Jaenecke, E. bezeichnet. Als Beispiel für ein solches Diagramm soll das eines Gemischs aus Na+-K+-NO3--SO42--H2O bei 25 °C aus Abbildung 11 besprochen werden. Auf der y-Achse sind die auf die Ladungsäquivalente bezogenen Molenbrüche der Nitrationen dargestellt, auf der x-Achse die der Kaliumionen. Alle Mischungen werden durch die auf die Ladungsäquivalente bezogenen Molenbrüche dargestellt, da auf diese Weise die Wertigkeit der Ionen berücksichtigt werden kann. Das bedeutet im Falle dieses Diagramms, dass sämtliche Mischungen als Teilbeitrag der Kalium-Kationen beziehungsweise der Nitrat-Anionen zur Gesamtmenge positiver beziehungsweise negativer Ladungen dargestellt werden. Beispielsweise leuchtet ein, dass bei sehr geringen Stoffmengenanteilen an Kalium- und Nitrat-Ionen Natrium- und Sulfat-Ionen überwiegen. Somit liegen in den Ecken die vier reinen Salze vor. Unten links Natriumsulfat, oben links Natriumnitrat, oben rechts Kaliumnitrat und unten rechts Kaliumsulfat. Die Felder innerhalb des Diagramms zeigen die Stabilitätsfelder der möglichen Phasen. Sie werden durch Linien getrennt, durch die die Sättigungskonzentrationen von Lösungen angegeben werden, bei denen die jeweils angrenzenden Phasen im Gleichgewicht vorliegen. Das heißt, dass innerhalb eines Feldes nur Sättigung in Bezug auf eine einzige Phase vorliegt, an Schnittpunkten von Sättigungskurven liegen drei Phasen gemeinsam im Gleichgewicht vor. An diesen Schnittpunkten liegen isotherme invariante Phasen vor (Phasenregel) [Steiger.etal:2014]Titel: Weathering and Deterioration
bezeichnet. Als Beispiel für ein solches Diagramm soll das eines Gemischs aus Na+-K+-NO3--SO42--H2O bei 25 °C aus Abbildung 11 besprochen werden. Auf der y-Achse sind die auf die Ladungsäquivalente bezogenen Molenbrüche der Nitrationen dargestellt, auf der x-Achse die der Kaliumionen. Alle Mischungen werden durch die auf die Ladungsäquivalente bezogenen Molenbrüche dargestellt, da auf diese Weise die Wertigkeit der Ionen berücksichtigt werden kann. Das bedeutet im Falle dieses Diagramms, dass sämtliche Mischungen als Teilbeitrag der Kalium-Kationen beziehungsweise der Nitrat-Anionen zur Gesamtmenge positiver beziehungsweise negativer Ladungen dargestellt werden. Beispielsweise leuchtet ein, dass bei sehr geringen Stoffmengenanteilen an Kalium- und Nitrat-Ionen Natrium- und Sulfat-Ionen überwiegen. Somit liegen in den Ecken die vier reinen Salze vor. Unten links Natriumsulfat, oben links Natriumnitrat, oben rechts Kaliumnitrat und unten rechts Kaliumsulfat. Die Felder innerhalb des Diagramms zeigen die Stabilitätsfelder der möglichen Phasen. Sie werden durch Linien getrennt, durch die die Sättigungskonzentrationen von Lösungen angegeben werden, bei denen die jeweils angrenzenden Phasen im Gleichgewicht vorliegen. Das heißt, dass innerhalb eines Feldes nur Sättigung in Bezug auf eine einzige Phase vorliegt, an Schnittpunkten von Sättigungskurven liegen drei Phasen gemeinsam im Gleichgewicht vor. An diesen Schnittpunkten liegen isotherme invariante Phasen vor (Phasenregel) [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Als Anwendungsbeispiel soll eine Lösungszusammensetzung von Punkt A betrachtet werden. Dieser liegt im Stabilitätsfeld von Glaserit (NaK3(SO4)2), so dass diese Phase bei Eindunstung der Lösung zuerst auskristallisieren würde. Durch die Kristallisation verändert sich bei voranschreitender Verdunstung die Lösungszusammensetzung, wobei die beteiligten Ionen proportional zu ihrem Vorkommen im auskristallisierenden Salz der Lösung entzogen werden. Dies erfolgt entlang der Linie A-B. An Punkt B liegt auch Sättigung in Bezug auf Thenardit vor, so dass die beiden Salze gemeinsam auskristallisieren. Durch weitere Kristallisation der beiden Phasen verändert sich die Lösungszusammensetzung weiter, und zwar entlang der Linie B-C. An diesem Punkt ist auch Sättigung in Bezug auf Darapskit (Na3NO3SO4∙H2O) erreicht. Da es sich bei dem Punkt jedoch um einen invarianten Punkt handelt, liegen nur dort die drei Phasen gemeinsam vor. Beim weiteren Eindunsten der Lösung muss Thenardit sich auflösen, da sein Stabilitätsfeld beim Verlauf entlang C-D verlassen wird. Endpunkt der Kristallisation ist der invariante Punkt D [Steiger:2009a]Titel: Modellierung von Phasengleichgewichten
Autor / Verfasser: Steiger, Michael [Steiger.etal:2008c]Titel: An improved model incorporating Pitzer's equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
[Steiger.etal:2008c]Titel: An improved model incorporating Pitzer's equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
Autor / Verfasser: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas .
.
Autor / Verfasser: Steiger, Michael
 , berechnet nach [Steiger.etal:2008c]Titel: An improved model incorporating Pitzer's equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code
, berechnet nach [Steiger.etal:2008c]Titel: An improved model incorporating Pitzer's equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program codeAutor / Verfasser: Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas
 .
.
Aussagekraft haben diese Phasendiagramme neben der Ableitung von Kristallisationsabfolgen aber noch in anderer Hinsicht. Die Größe der Stabilitätsfelder verschiedener Phasen geben Hinweise darüber, wie wahrscheinlich es ist, dass diese Phase aus dem Gemisch auskristallisiert. Je größer das Feld, desto mehr Zusammensetzungen können zur Phasenbildung führen. Außerdem ist es wichtig ableiten zu können, welche Phasen des Gemischs gemeinsam vorliegen können. Nur aneinander grenzende oder durch invariante Punkt verbundene Phasen können gemeinsam auftreten. Somit wäre es in dem besprochenen Beispiel nicht möglich, Mirabilit zusammen mit Kaliumnitrat oder Kaliumsulfat zu identifizieren [Steiger.etal:2014]Titel: Weathering and Deterioration
Autor / Verfasser: Steiger, Michael; Charola A. Elena; Sterflinger, Katja .
.
Literatur[Bearbeiten]
| [Arnold.etal:1991] | Arnold, Andreas; Zehnder, Konrad (1991): Monitoring Wall Paintings Affected by soluble Salts. In: Cather, Sharon (Hrsg.): The Conservation of Wall Paintings: Proceedings of a symposium organized by the Coutrauld Institut of Art and the Getty Conservation Institute, London, July 13-16, The Getty Conservation Institute, 103-136, Webadresse. |  |
| [Espinosa.etal:2008] | Espinosa, R.; Franke, L.; Deckelmann, G. (2008): Model for the mechanical stress due to the salt crystallization in porous materials. In: Construction and Building Materials, 22 (7), 1350-1367, Webadresse, https://doi.org/10.1016/j.conbuildmat.2007.04.013 |  |
| [Genkinger.etal:2007] | Genkinger, Selma; Putnis, Andrew (2007): Crystallisation of sodium sulfate: supersaturation and metastable phases. In: Environmental Geology, 52 (2), 329-337, Webadresse, https://doi.org/10.1007/s00254-006-0565-x |  |
| [Grossi.etal:2013] | Grossi, C.M.; Esbert, R.M.; Suarez del Rio, L.M.; Montoto, M.; Laurenzi-Tabasso, M. (2013): Acoustic emission monitoring to study sodium sulphate crystallization in monumental porous carbonate stones. In: Studies in Conservation, 42 (2), 115-125, Webadresse, https://doi.org/10.1179/sic.1997.42.2.115 |  |
| [Jaenecke:1906] | Jaenecke, E. (1906): Über eine neue Darstellungsform der wässerigen Lösungen zweier und dreier gleichioniger Salze, reziproker Salzpaare und der van't Hoffschen Untersuchungen über ozeanische Salzablagerungen.. In: Z. Anorg. Allg. Chem., 51 (), 132 |  |
| [Linnow.etal:2006] | Linnow, Kirsten; Zeunert, Anke; Steiger, Michael (2006): Investigation of Sodium Sulfate Phase Transitions in a Porous Material Using Humidity- and Temperature-Controlled X-ray Diffraction. In: Analytical Chemistry, 78 (13), 4683-4689, Webadresse, https://doi.org/10.1021/ac0603936 |  |
| [Price.etal:1994] | Price, Clifford A.; Brimblecomb, Peter (1994): Preventing salt damage in porous materials. In: Roy, A.; Smith, P. (Hrsg.): Preventive conservation: practice, theory and research. Preprints of the contributions to the Ottawa Congress, 12-16 September 1994, International Institute for Conservation of Historic and Artistic Works, 90-93, Webadresse. |  |
| [Steiger.etal:1995] | Steiger, Michael; Dannecker, Walter (1995): Hygroskopische Eigenschaften und Kristallisationsverhalten von Salzgemischen. In: Snethlage, Rolf (Hrsg.): Jahresberichte Steinzerfall - Steinkonservierung für 1993, Verlag Ernst & Sohn, 115-128. |  |
| [Steiger.etal:1996] | Steiger, M.; Zeunert, A. (1996): Crystallization properties of salt mixtures: comparison of experimental results and model calculations. In: Riederer, J. (Hrsg.): Proceedings of the 8th International Congress on Deterioration and Conservation of Stone,Möller Druck 535-544. |  |
| [Steiger.etal:2008] | Steiger, Michael; Asmussen, Sönke (2008): Crystallization of sodium sulfate phases in porous materials: The phase diagram Na2SO4 -H2O and the generation of stress. In: Geochimica et Cosmochimica Acta, 72 (17), 4291-4306, Webadresse, https://doi.org/10.1016/j.gca.2008.05.053 |  |
| [Steiger.etal:2008c] | Steiger, Michael; Kiekbusch, Jana; Nicolai, Andreas (2008): An improved model incorporating Pitzer's equations for calculation of thermodynamic properties of pore solutions implemented into an efficient program code. In: Construction and Building Materials, 22 (8), 1841-1850, Webadresse, https://doi.org/10.1016/j.conbuildmat.2007.04.020 |  |
| [Steiger.etal:2014] | Steiger, Michael; Charola A. Elena; Sterflinger, Katja (2014): Weathering and Deterioration. In: Siegesmund S.; Snethlage R. (Hrsg.): Stone in Architecture, Springer Verlag Berlin Heidelberg, 223-316, Webadresse, https://doi.org/10.1007/978-3-642-45155-3_4. |  |
| [Steiger:2009a] | Steiger, Michael (2009): Modellierung von Phasengleichgewichten. In: Schwarz, Hans-Jürgen; Steiger, Michael (Hrsg.): Salzschäden an Kulturgütern: Stand des Wissens und Forschungsdefizite, Ergebnisse des DBU Workshops im Februar 2008 in Osnabrück, Deutsche Bundesstiftung Umwelt, Hannover, 80-99, Webadresse. |   |
| [Xu.etal:1999] | Xu B., Schweiger G. (1999): In-situ Raman observations of phase transformation of Na2SO4 during the hydration/dehydration cycles on single levitated microparticle.. In: J. Aerosol. Sci., (), 379-380, Webadresse, https://doi.org/10.1016/S0021-8502(99)80201-8 |  |